| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13014 | Happy A to B |
|
| 14129 | Climbing Stairs part 1 |
|
| 14130 | Climbing Stairs part 2 |
|
| 14139 | Chess Puzzle part 1 |
|
| 14140 | Chess Puzzle part 2 |
|
| 14141 | Chess Puzzle part 3 |
|
Description
Let's call a grid 8-puzzle board if the gridsize is 3 x 3 and there is exactly one cell is 'x' and others are '1' or '0'.
In one operation, you can exchange the 'x' cell of a 8-puzzle board with any cell which is adjacent to the 'x' cell. The cell (i, j) is adjacent to the cell (i-1, j), (i, j-1), (i, j+1) and (i+1, j).
Now you need to solve T tasks. In each task, you are given two 8-puzzle boards A, B and one integer K. You need to answer whether it's possible to make A into B in at most K operations.
Let's take an example. In the first task of Sample, you can make A into B in the following 2 operations:
0 x 0 0 0 x 0 0 1
1 0 1 ========> 1 0 1 ========> 1 0 x
0 1 1 0 1 1 0 1 1
exchange (1,3) exchange (2,3)
Input
The first line contains an integer T (1 ≤ T ≤ 10) – the number of tasks you need to solve.
And for each task, first you are given one integer K (0 ≤ K ≤ 9) – the maximum number of operations you can execute. Then you are given A and B. Both of them are in 3 lines of 3 characters. Please refer to Sample Input.
Output
For each task output "Yes" if it's possible to make A into B in K operations. Otherwise output "No". Then print a newline('\n').
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are climbing a staircase. It takes N steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

(e.g., For n=2, there are 2 ways to reach the top:[1,1] and [2])
In this problem, there will be T testcases to check.
If you got TLE on the testcase 3 and 4, please consider using dynamic programming.
Input
The first line is T, the number of Ns.
And the following T lines are Ns, the heights of the stairs.
There are different ranges for the four test cases:
Test case 1: (1<T<20) and (1< every step N in Ns < 10)
Test case 2: (1<T<20) and (1< every step N in Ns < 45)
Test case 3&4: (1<T<=10000) and (1< every step N in Ns < 45)
Output
T solutions ended with a newline character.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Similar to 14129- Climbing Stairs part 1, each time you can either climb 1 or 2 steps.
However, in this problem, you are given an integer array cost where cost[i] is the cost of ith step on a staircase.
After you pay the cost, you can either climb one or two steps.
You asked to calculate the minimum cost to reach Nth stairs.
Note that you can start from index 0 or index 1 in this problem.
For example,
If cost = [1,100,1,1,1,100,1,1,100,1],
You will start at index 0. - Pay 1 and climb two steps to reach index 2. - Pay 1 and climb two steps to reach index 4. - Pay 1 and climb two steps to reach index 6. - Pay 1 and climb one step to reach index 7. - Pay 1 and climb two steps to reach index 9. - Pay 1 and climb one step to reach the top. The total cost is 6.
Input
There are T Ns in this problem.
The first line is an integer T, the number of testcases.
The second line is an integer C, the number of costs.
The third line are C integers costs, where (1<= the value of the cost <= 999).
And the following T lines are the heights of the stairs.
For test case 1 on OJ: (1<=T<=5) and (1<=C<=10).
For test case 2 on OJ: (1<=T<=100) and (1<=C<=100).
Output
T solutions ended with a newline character.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Domo is a brilliant dog. Now he needs to solve these problems to pass the I2P.
In the mid2 practice, Domo has solved the N-Queens M-Rooks Problem, but now, there are some variant problems that need your help to finish.
Note: This problem is separated into three parts, each with different constraints. The differences between each part will be highlighted in red.
The first part of the chess puzzle is N-Queens M-Rooks Problem.
You need to find how many ways to place N queens and M rooks on an (N+M) × (N+M) chessboard such that no two of queens or rooks can attack each other in 1 step.
For N = 1, M = 2, there're 4 solutions:
( 0 means empty spot, Q means queen, R means rook. )
Q 0 0 0 R 0
0 0 R R 0 0
0 R 0 0 0 Q
0 R 0 0 0 Q
0 0 R R 0 0
Q 0 0 0 R 0
Possible move of Queen:
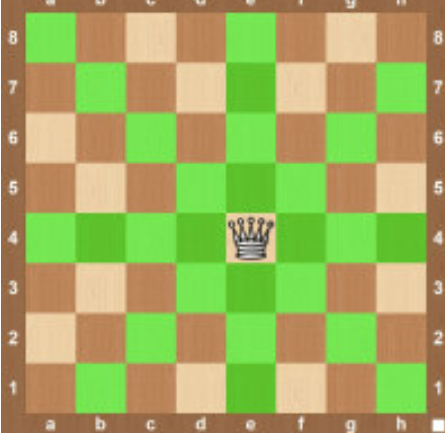
Possible move of Rook:

Input
The first line consists of an integer T (1 ≤ T ≤ 10) indicating the number of test cases.
For the next T lines, each line consists of two integer N and M (1 ≤ N, M ≤ 9, 1 ≤ N+M ≤ 9)
Output
For each test case, output the number of ways that you can place chesses.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Domo is a brilliant dog. Now he needs to solve these problems to pass the I2P.
In the mid2 practice, Domo has solved the N-Queens M-Rooks Problem, but now, there are some variant problems that need your help to finish.
Note: This problem is separated into three parts, each with different constraints. The differences between each part will be highlighted in red.
The first part of the chess puzzle is N-Queens M-Rooks Problem with threshold.
You need to find how many ways to place N queens and M rooks on an (N+M) × (N+M) chessboard such that no two of queens or rooks can attack each other in 1 step.
In addition, there's an integer in each block on the chessboard. The sum of the blocks where you place a chess piece cannot exceed K.
For N = 1, M = 2, K = 5, and the chessboard is shown below:
1 1 6 1 1 1 1 1 1
There're 3 solutions:
( 0 means empty spot, Q means queen, R means rook. )
Q 0 0 0 R 0
0 0 R R 0 0
0 R 0 0 0 Q
0 R 0
0 0 R
Q 0 0
Notice that this is not a solution, since the sum of blocks is 8 (but K is 5).
0 0 Q | 1 1 6 R 0 0 | 1 1 1 0 R 0 | 1 1 1
Possible move of Queen:
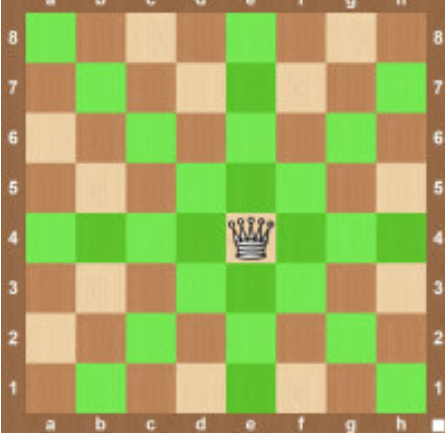
Possible move of Rook:

Input
The first line consists of an integer T (1 ≤ T ≤ 10) indicating the number of test cases.
Starting from the second line, the input will be test cases.
For each test case, the first line consists of three integers N, M, and K (1 ≤ N, M ≤ 9, 1 ≤ N+M ≤ 9, 1 ≤ K ≤ 1000)
For the next N+M line, each line consists of N+M numbers A1, A2, ..., AN+M, indicating integers in the chessboard. (1 ≤ Ai ≤ 1000)
Output
For each test case, output the number of ways that you can place chesses.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Domo is a brilliant dog. Now he needs to solve these problems to pass the I2P.
In the mid2 practice, Domo has solved the N-Queens M-Rooks Problem, but now, there are some variant problems that need your help to finish.
Note: This problem is separated into three parts, each with different constraints. The differences between each part will be highlighted in red.
The second part of the chess puzzle is N-Knights M-Rooks Problem.
You need to find how many ways to place N knights and M rooks on an (N+M) × (N+M) chessboard such that no two of knight or rook can attack each other in 1 step, and each row and each column contains exactly one knight or one rook.
For N = 2, M = 1, there're 6 solutions:
( 0 means empty spot, R means rook, K means knight. )
R 0 0 0 0 R K 0 0
0 K 0 0 K 0 0 R 0
0 0 K K 0 0 0 0 K
0 0 K K 0 0 0 0 K
0 K 0 0 K 0 0 R 0
R 0 0 0 0 R K 0 0
Note: This is not a valid solution. While none of the two chess can attack each other, we need to ensure that each row and each column contains exactly one chess.
0 R 0 K 0 K 0 0 0
Possible move of Rook:

Possible move of Knight:

Input
The first line consists of an integer T (1 ≤ T ≤ 10) indicating the number of test cases.
For the next T lines, each line consists of two integer N and M (1 ≤ N, M ≤ 9, 1 ≤ N+M ≤ 9)
Output
For each test case, output the number of ways that you can place chesses.