| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12604 | N-Queens M-Rooks Problem |
|
| 13014 | Happy A to B |
|
| 13420 | Domo travels around the world |
|
| 14102 | Domo's 3D Maze |
|
| 14109 | HUTI |
|
| 14120 | A Dorm is Approaching |
|
Description
N queens problem asks how many ways to place N non-attacking queens on an N×N chessboard.
For example, there’re 2 solutions for N = 4:
( 0 means empty spot, Q means queen. )
0 Q 0 0 0 0 Q 0
0 0 0 Q Q 0 0 0
Q 0 0 0 0 0 0 Q
0 0 Q 0 0 Q 0 0
While, there’s no solution for N = 2:
Below is the all placements. All of them contains queens threaten each other.
Q Q Q 0 Q 0 0 Q 0 Q 0 0
0 0 Q 0 0 Q Q 0 0 Q Q Q
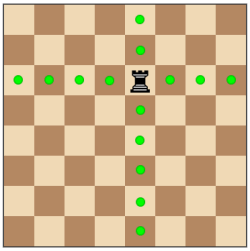
Let’s define a new problem “N-Queens M-Rooks Problem”.
It asks how many ways to place N queens and M rooks on an (N+M)×(N+M)( chessboard such that no two of queens or rooks can attack each other in 1 step.
For N = 1, M = 2, there’re 4 solutions:
( 0 means empty spot, Q means queen, R means rook. )
Q 0 0 0 R 0
0 0 R R 0 0
0 R 0 0 0 Q
0 R 0 0 0 Q
0 0 R R 0 0
Q 0 0 0 R 0
Possible move of Queen:

Possible move of Rook:
Input
There’re multiple testcases.
Each testcase is consisted of 2 integers N,M on one line.
It’s guaranteed that:
- 0 ≤ N, M ≤ 9
- 1 ≤ N+M ≤ 9
Output
Print the number of solution for N-Queens M-Rooks Problem for every testcase.
Remember ‘\n’ on the end of line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Let's call a grid 8-puzzle board if the gridsize is 3 x 3 and there is exactly one cell is 'x' and others are '1' or '0'.
In one operation, you can exchange the 'x' cell of a 8-puzzle board with any cell which is adjacent to the 'x' cell. The cell (i, j) is adjacent to the cell (i-1, j), (i, j-1), (i, j+1) and (i+1, j).
Now you need to solve T tasks. In each task, you are given two 8-puzzle boards A, B and one integer K. You need to answer whether it's possible to make A into B in at most K operations.
Let's take an example. In the first task of Sample, you can make A into B in the following 2 operations:
0 x 0 0 0 x 0 0 1
1 0 1 ========> 1 0 1 ========> 1 0 x
0 1 1 0 1 1 0 1 1
exchange (1,3) exchange (2,3)
Input
The first line contains an integer T (1 ≤ T ≤ 10) – the number of tasks you need to solve.
And for each task, first you are given one integer K (0 ≤ K ≤ 9) – the maximum number of operations you can execute. Then you are given A and B. Both of them are in 3 lines of 3 characters. Please refer to Sample Input.
Output
For each task output "Yes" if it's possible to make A into B in K operations. Otherwise output "No". Then print a newline('\n').
Sample Input Download
Sample Output Download
Tags
Discuss
Description

(Domo's friend Kao who gives him the VIP service)
Domo is a brilliant dog, but after this semester, he is very tired and needs to have some rest. Hence, he wants to travel around the world.
Luckily, Domo's friend gives him the VIP service, which can have a flight for free between some cities.
Now, given the number of cities and the free flight list, and Domo starts its travel from the city 0, please find out that how many tickets Domo needs to buy to travel to all the cities (you need 1 ticket to travel from one city to another).
For example, the sample gives 6 cities and 4 pairs of free flights (black line) shown as below:
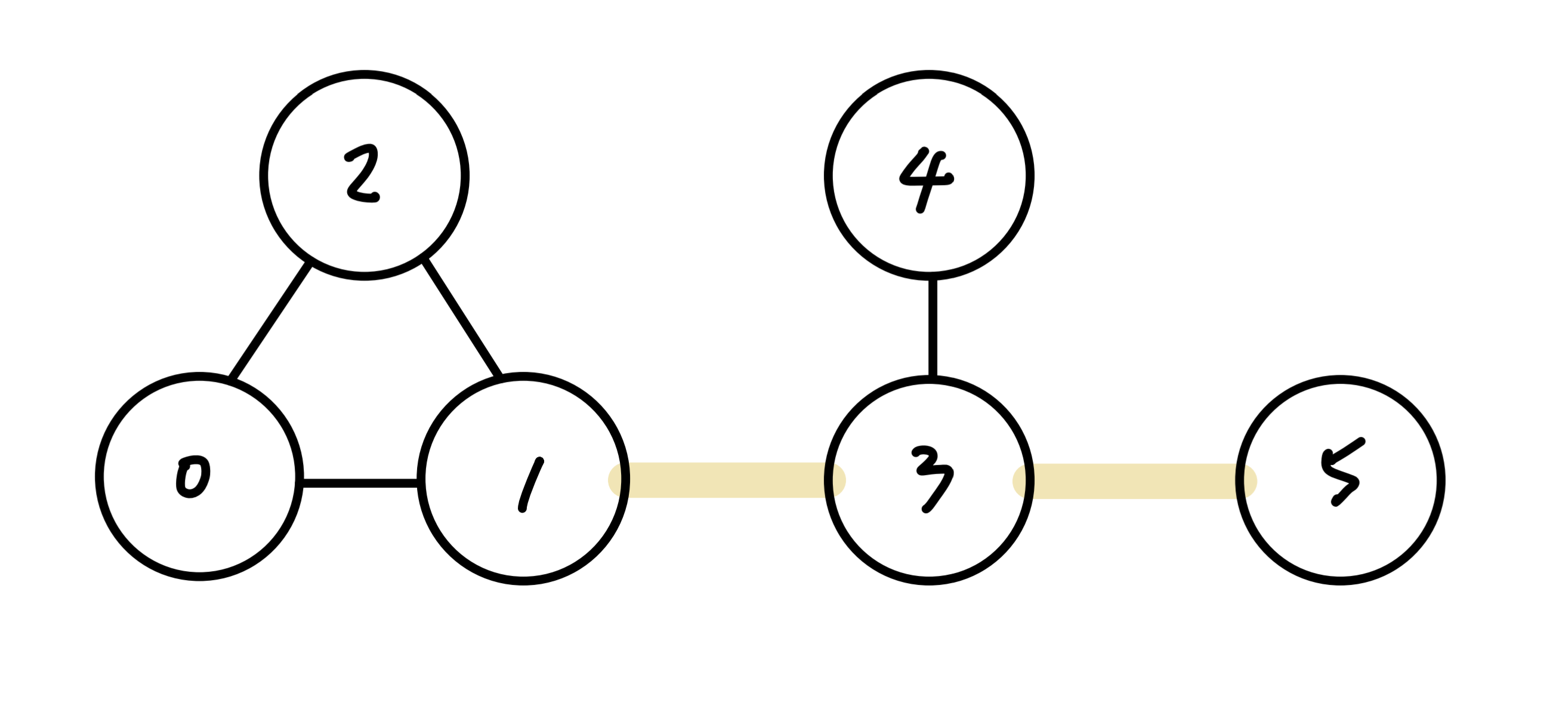
We need at least two tickets to travel to all the cities (for example, from 1 to 3 and from 3 to 5), hence the answer is 2.
There are two hints for this problem:
Hint 1: (You might get 3/6 with this hint)
If there isn't any cycle on the map, we can directly find the answer using the integer N and K.
In other words, you don't need to consider what the graph looks like, since we can list an equation for the answer with the integer N and K.
Hint 2 : (Complete solution. You may solve this problem with this hint)
visit[] // check whether every city has been visited.
count = 0;
while (!visit_all_cities) {
pick_one_unvisited_city(); // pick an unvisited city.
mark_free_cities(); // mark all the cities we can travel from this city without any ticket.
count++; // increase the group count.
}
ans = ? // find out the relation between the answer and the group count!
Input
The first line consists of two numbers N (1 ≤ N ≤ 100) and K (1 ≤ K ≤ N⋅(N-1)/2) - denoting that there are N cities in the world.
For the next K lines, each line contains two numbers A, B (0 ≤ A, B < N) - denoting that Domo can have a free flight between A and B (A ↔ B).
Output
Print the minimum number of tickets that Domo needs to buy to travel around all the cities.
Remember to print an '\n' at the end of the line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Domo is a brilliant dog. One day, he accidentally gets trapped in a maze with multiple floors. Let's find the shortest path for him to escape!
This maze is cube-like, with each block, except the barricade blocks, containing an integer that represents the time required to pass through it.
When you want to exit this maze, the time you spend will be the sum of integers on your path from the start to the exit, including the starting block and the exit block.
You can move only right, forward, and down from every position. However, please note that you cannot move into a barricade block or move out of the cube.
i.e.: If you are at pos[i][j][k], you can move to three positions (only when it's inside the cube and not a barricade):
- pos[i+1][j][k]
- pos[i][j+1][k]
- pos[i][j][k+1]
If the size of this cube is N * M * K, the exit is always at position maze[N-1][M-1][K-1], and you always start from maze[0][0][0].
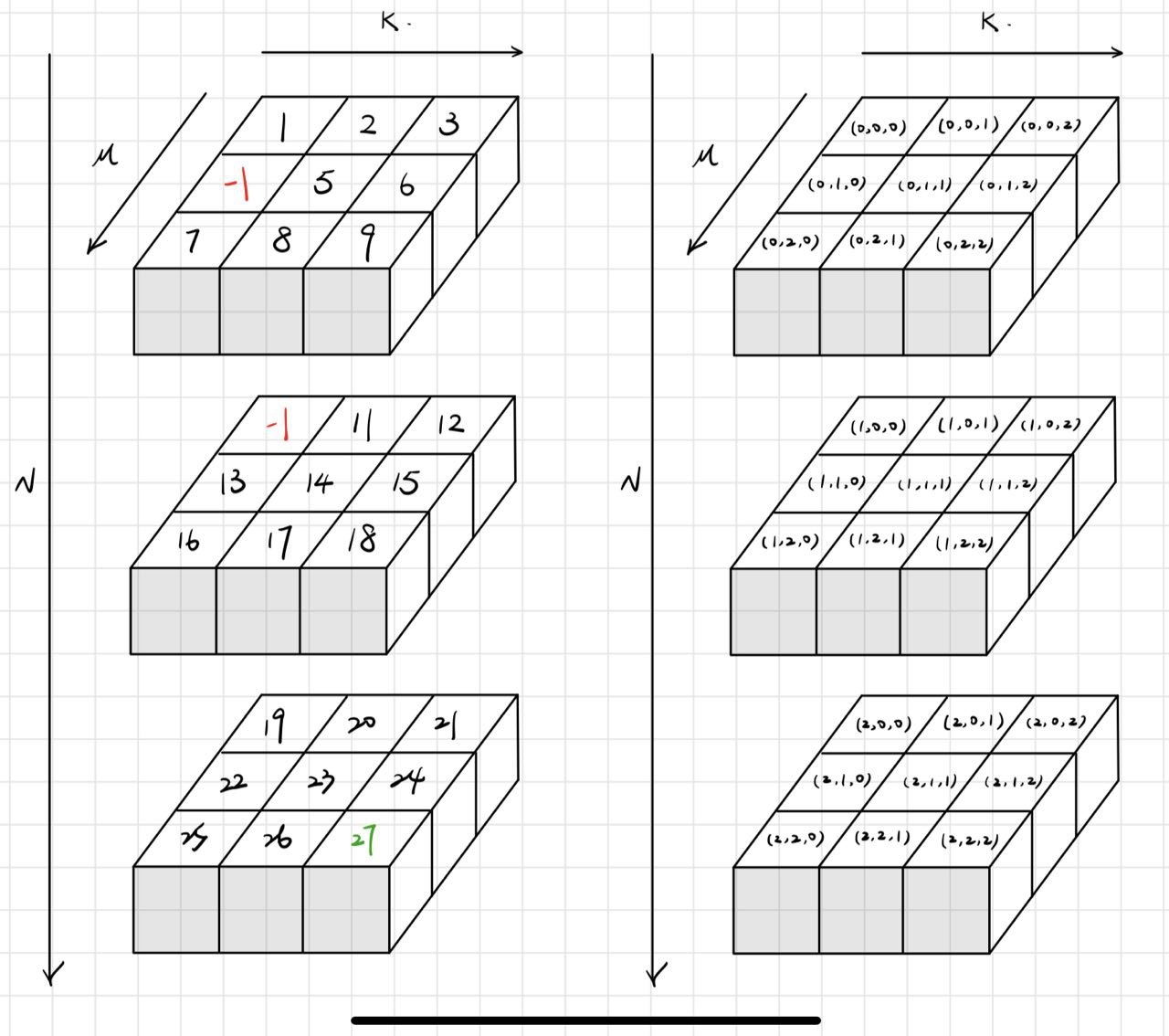
For example, in a 3 * 3 * 3 maze, with the cost of each block and barricades shown below, the shortest path to the exit would be [1, 2, 3, 6, 9, 18, 27], and the cost would be 66.
In this picture, the left side indicates the time you spend on the block, and the right side indicates the index of each block.
Input
The first line consists of three integers N, M, K (1 ≤ N, M, K ≤ 100), describing the size of the maze. The number of floors is N, and each floor is M * K.
For the next N * M lines, each line contains K integers A1, A2, ..., Ak, describing the layout of the maze. (1 ≤ Ai ≤ 100 or Ai is -1)
If Ai is -1, it indicates that the block is a barricade, and you cannot enter that block.
Lines 2 through M+1 describe the layout of the first floor,
lines M+2 through 2M+1 describe the layout of the second floor,
and so on.
Output
Output the minimum cost of the time you spend to exit this maze. Remember to print a newline character at the end of the line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There is a well-known method to describe personality, which is MBTI(Myers-Briggs Type Indicator).
One day, TAs of I2P(I) want to develop their own TI, which is called "HUTI".
We'll use a integer to record the index of each personality type.

To check which type is the most unique one, given a type sequence, the most unique one is the one with an odd number of occurrences
For example, the unique number in [1, 3, 2, 3, 2] is 1.
Following the above rule, we'll check N students and the results will be used to determine the most unique type in the class.
Note:
Use an "XOR" operation in this problem.
If you need more details, you can check : this
Input
The input is composed of two parts.
The first line is N (1<=N<=100000001).
The following N lines will be the type indexes (The integer will be less or equal to 100000000).
Output
The unique type ended with a new line character.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Vigilis a master builder with a unique specialization: Dorms. When building a dorm, Vigil always builds it with a width of 2 and a height of n. Vigil also can create an unlimited amount of building materials of any width and height as long as they are integers.

In every contract, Vigil is given a height n and is told to build every variation of the dorm with width 2 and height n ( mirrored and rotated dorms are counted separately if they look different).
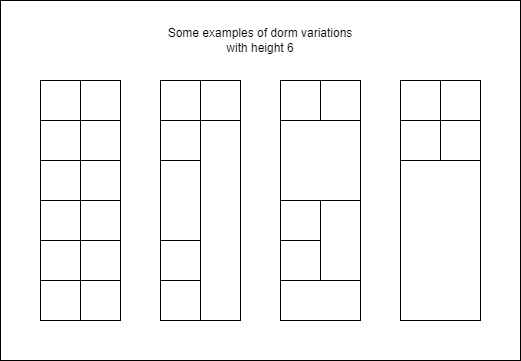
Help Vigil calculate how many different dorm variations there are given n.
Input
The first line contains the integer q (1 <= q <= 100).
The following q lines contain the n value, for the height of the tower (1 <= n <= 106).
Output
q lines, each line containing the number of dorm variations mod 109 + 7.