| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11711 | Dynamic 3D array |
|
| 12498 | Partial Judge Example |
|
| 13348 | DomoMaze - easy version |
|
| 14101 | Quick Select Algorithm |
|
Description
In this problem, you are asked to design two functions
1.
unsigned*** new_3d_array(unsigned n,unsigned m,unsigned k);
malloc an n*m*k 3D unsigned array, and then return its address. The main function will check the correctness of your array.
2.
void delete_3d_array(unsigned ***arr);
Free the memory space of your array that was previously allocated by using malloc. Be careful about the memory uage of your program allocated dynamically so as to avoid MLE.
The two functions have been declared in function.h, and you are asked to complete the function definitions in function.c.
Your program should construct the 3D array by using only three malloc function calls. Notice that malloc is a time-consuming operation.
Note: for OJ submission:
Step 1. Submit only your function.c into the submission block. (Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
Please refer to the main function.
The input only has one line, consisting of five positive integers t,n,m,k,r separated by space characters, where t is the number of tests, (n,m,k) represents the array size, and r is a parameter for testing.
Note that n*m*k<=10000000 and t*n*m*k<=60000000
Output
In order to test your array's correctness, we will use your array to do some computations and output the results.
Sample Input Download
Sample Output Download
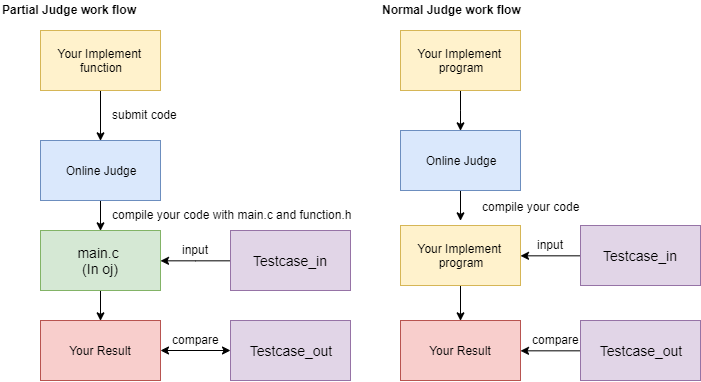
Partial Judge Code
11711.cPartial Judge Header
11711.hTags
Discuss
Description
This is the partial judge example (another method for online judge), you are asked to design a function below:
int call_add(int a, int b);
(implement a function to add two pass value togeter)
Note: for OJ partial judge submission:
Step 1. Submit only your function.c into the submission block. (Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
/* the content below is what you need to copy and submit to oj*/
int call_add(int a, int b){
return a + b;
}
More information about the different of partial judge and normal judge
Input
Please refer to the main function.
The input only one line, contain two number a and b (1 < a < 10, 1< b < 10)
Output
Output a + b.
Sample Input Download
Sample Output Download
Partial Judge Code
12498.cPartial Judge Header
12498.hTags
Discuss
Description

Domo is a brilliant dog. By the way, his grandfather is also a brilliant dog, and he has built a giant maze in the forest years ago, which is called "DomoMaze".
One day, Domo loses his ball called Wilson in this maze. He wants to take Wilson back, and your task is to find out how many ways Domo can reach the position where Wilson is.
This DomoMaze can be described as a two-dimensional array. With width W and length L, Domo is at the position (0, 0) in the beginning, and Wilson is at the position (W-1, L-1).
Each time Domo moves, he can choose one of three ways below:
1. from (i, k) to (i+1, k)
2. from (i, k) to (i, k+1)
3. from (i, k) to (i+1, k+1)
Also, there are some barricades in the maze. You can't enter the barricades on the map.
It is guaranteed that the barricade will not appear at (0, 0) and (W-1, L-1).
Given the size of DomoMaze and the position of all barricades, please find out how many ways Domo can find Wilson.
We introduced a method called Dynamic Programming.
The main idea is to use the answer of sub-problems to find out the answer to the original problem.
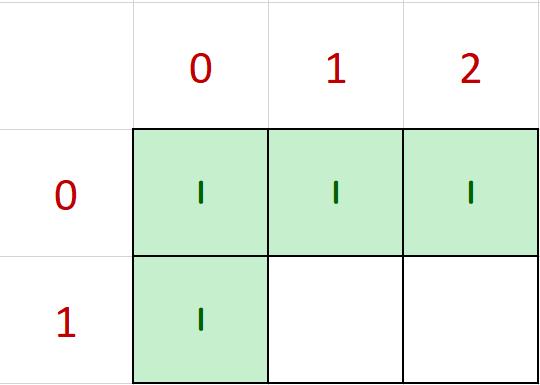
For example, a DomoMaze is given below:

We can calculate how many ways Domo can reach for every position. Obviously, for each position whose index of row or column is 0, there is only 1 way Domo can reach.
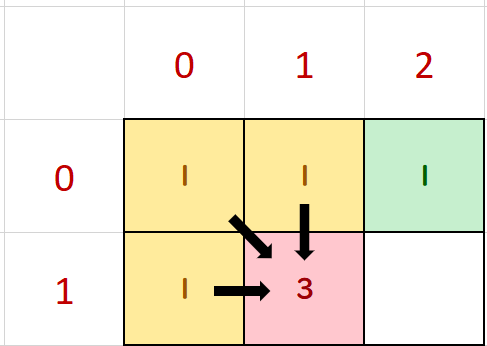
Next, we can calculate the ways Domo can reach the position (1, 1) with the following equation:
f(1, 1) = f(0, 0) + f(1, 0) + f(0, 1)
Hence, there are 3 ways Domo can reach the position (1, 1).
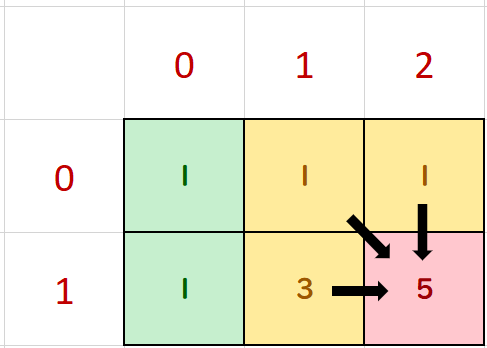
The last step, find the ways Domo can reach (1, 2), which is:
f(1, 2) = f(0, 1) + f(1, 1) + f(0, 2)
You can search dynamic programming on the internet for details if you still have questions.
Reference
English:
Dynamic Programming - GeeksforGeeks
What is the difference between bottom-up and top-down?
Mandarin:
Input
The first line contains two integers W (1 ≤ W ≤ 20) and L (1 ≤ L ≤ 20) - the width and the length of DomoMaze
For the next W lines, each line has L numbers either 1 or 0 - 0 for empty, and 1 for the barricade.
Output
The output only contains a number and a newline character - the number of ways Domo can reach where Wilson is.
It's guaranteed that the answer will not be greater than 263-1.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Quickselect is a powerful algorithm for finding the kth smallest element in an unordered list. It works by selecting any element from a list, which we will call a "pivot". Then, we can put every element "smaller" than the pivot to its left and every element "larger" than the pivot to its right. By doing so, we can determine whether the kth smallest element is to the left of the pivot, to the right of the pivot, or is the pivot. To demonstrate how it works, we will be asking you to implement two functions:
void SwapString(char **str1, char **str2);
This function should swap strings str1 and str2.
For example, if we have an array of fruit names A and we call SwapString(&A[2], &A[6]), the resulting array will be:
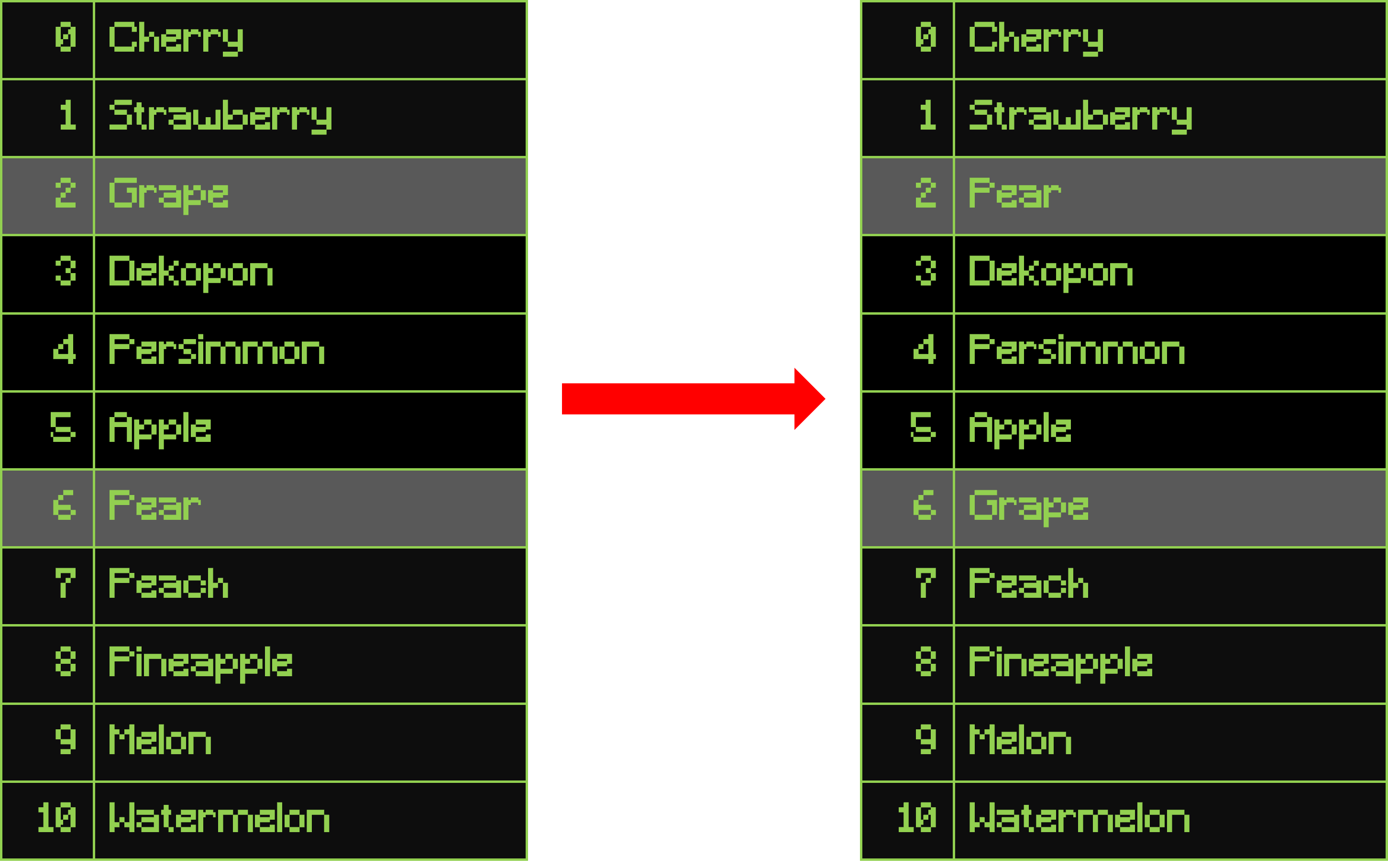
int Partition(char **A, int l, int r);
This function should choose any string from the index between l and r (inclusively) and use that string to partition the strings in the range. After that, return the index where your pivot ended up at.
For example, if we have an array of fruit names, A, and we call Partition(A, 2, 6), the resulting array might look like this:
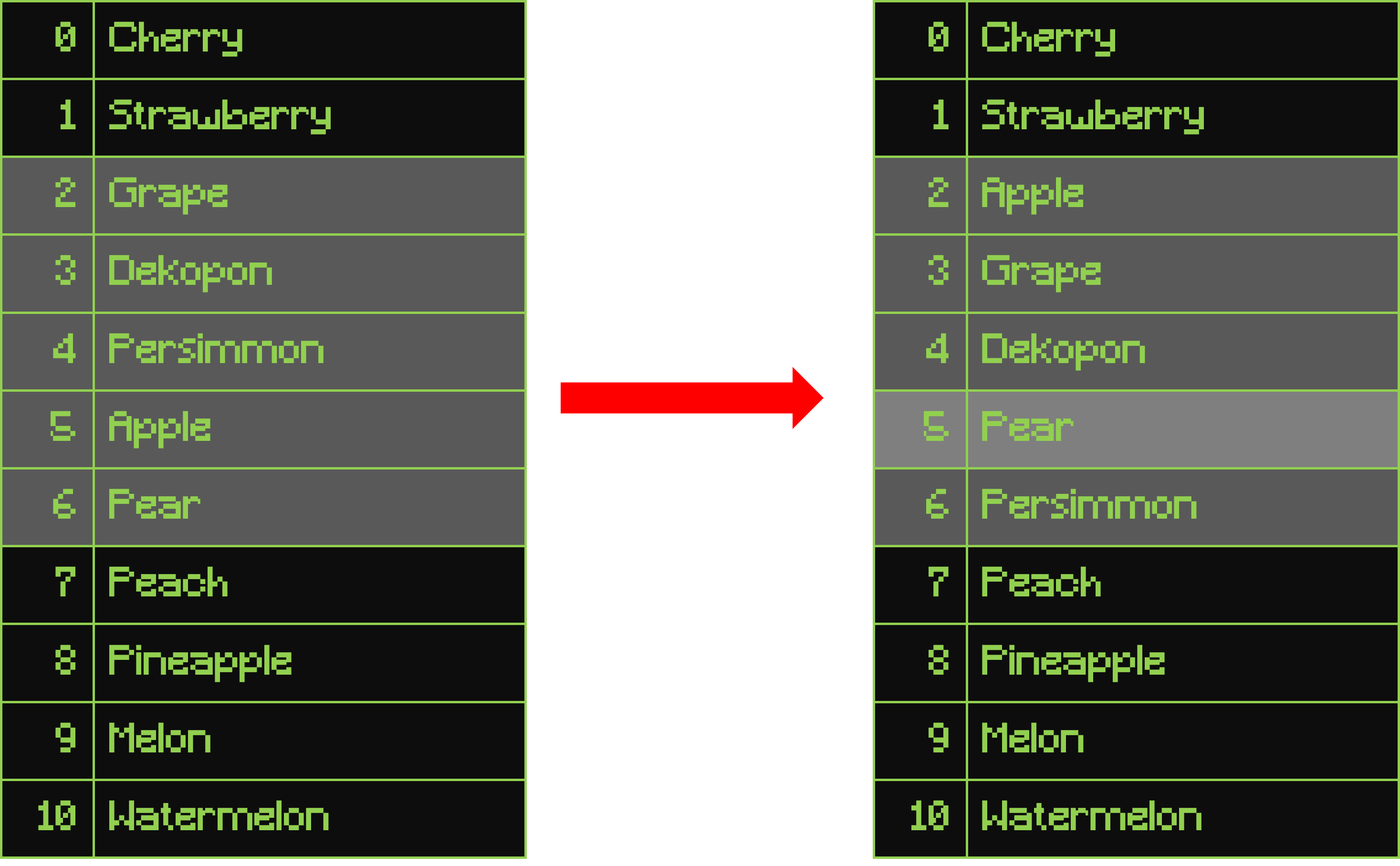
and the function will return 5, which is the index of the pivot ("Pear").
The QuickSelect algorithm works as follows:
Suppose we want to find the 4th smallest element (in human notation). First, a pivot is selected from a list:
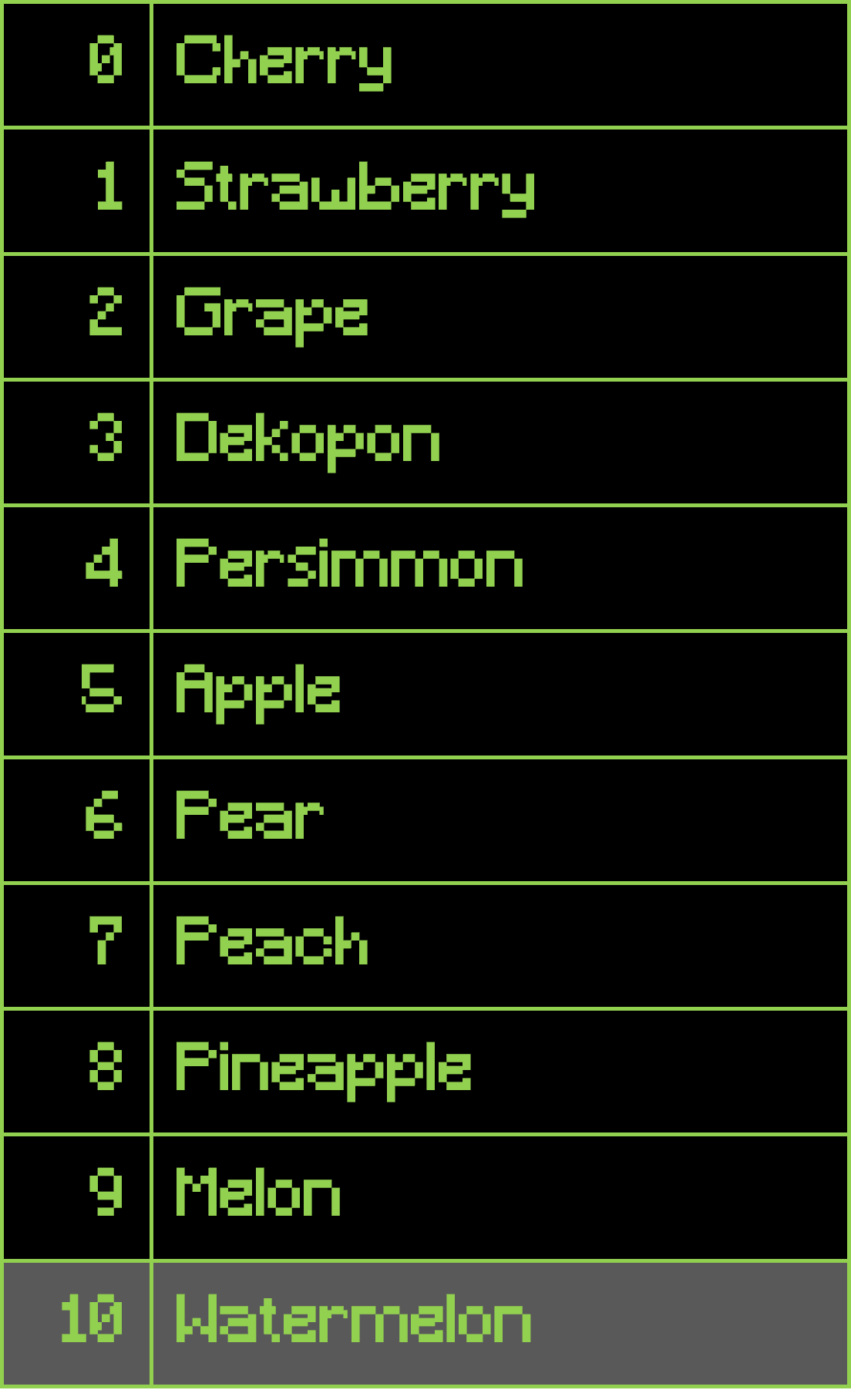
Then, all elements that come before the pivot are moved before it, and all elements that come after the pivot are moved after it. In this case, no elements come after "Watermelon", so the array looks the same.
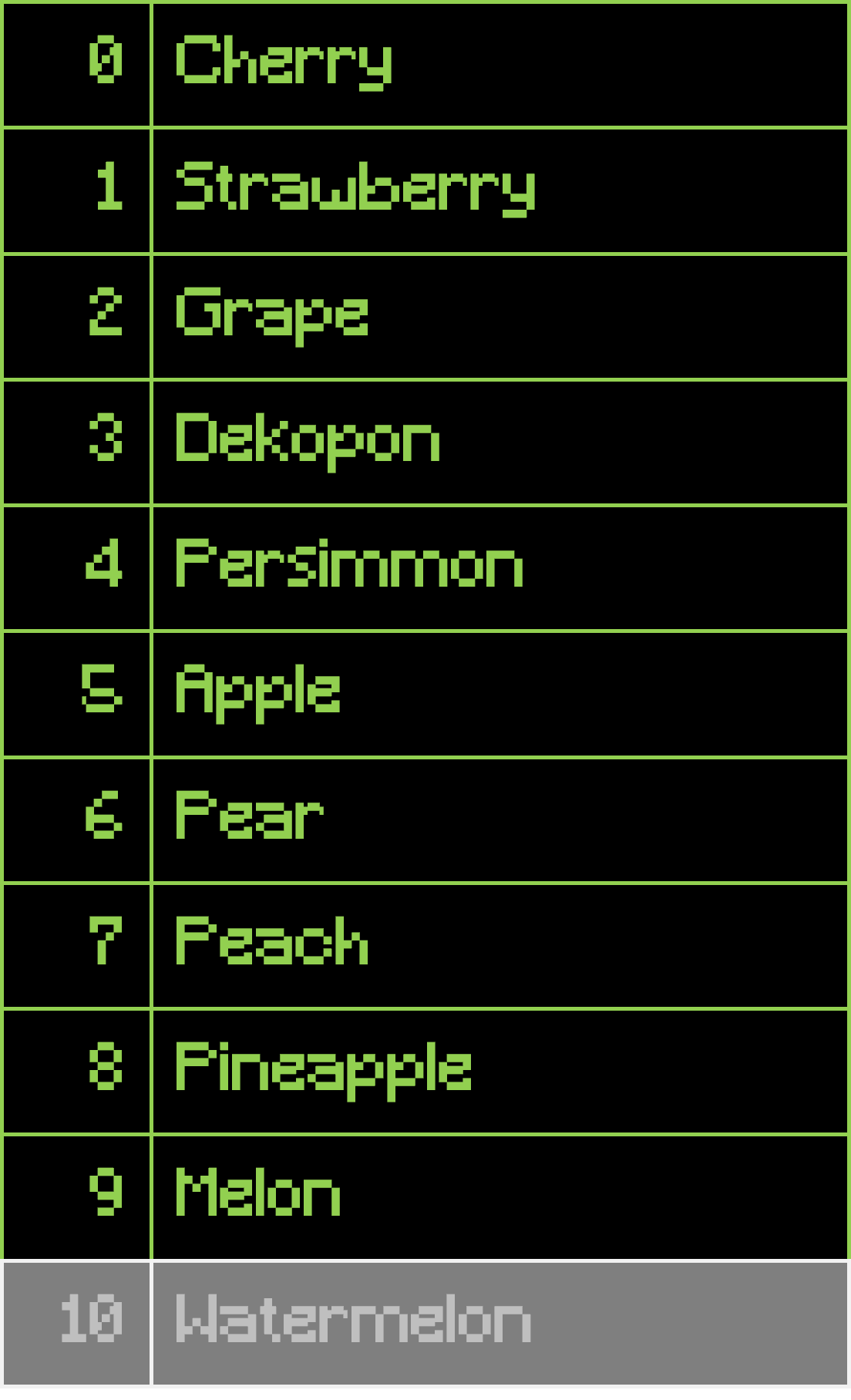
At this point, we know the smallest element is not the pivot nor after it, so we can repeat the same process on the array before the pivot. We select another pivot:
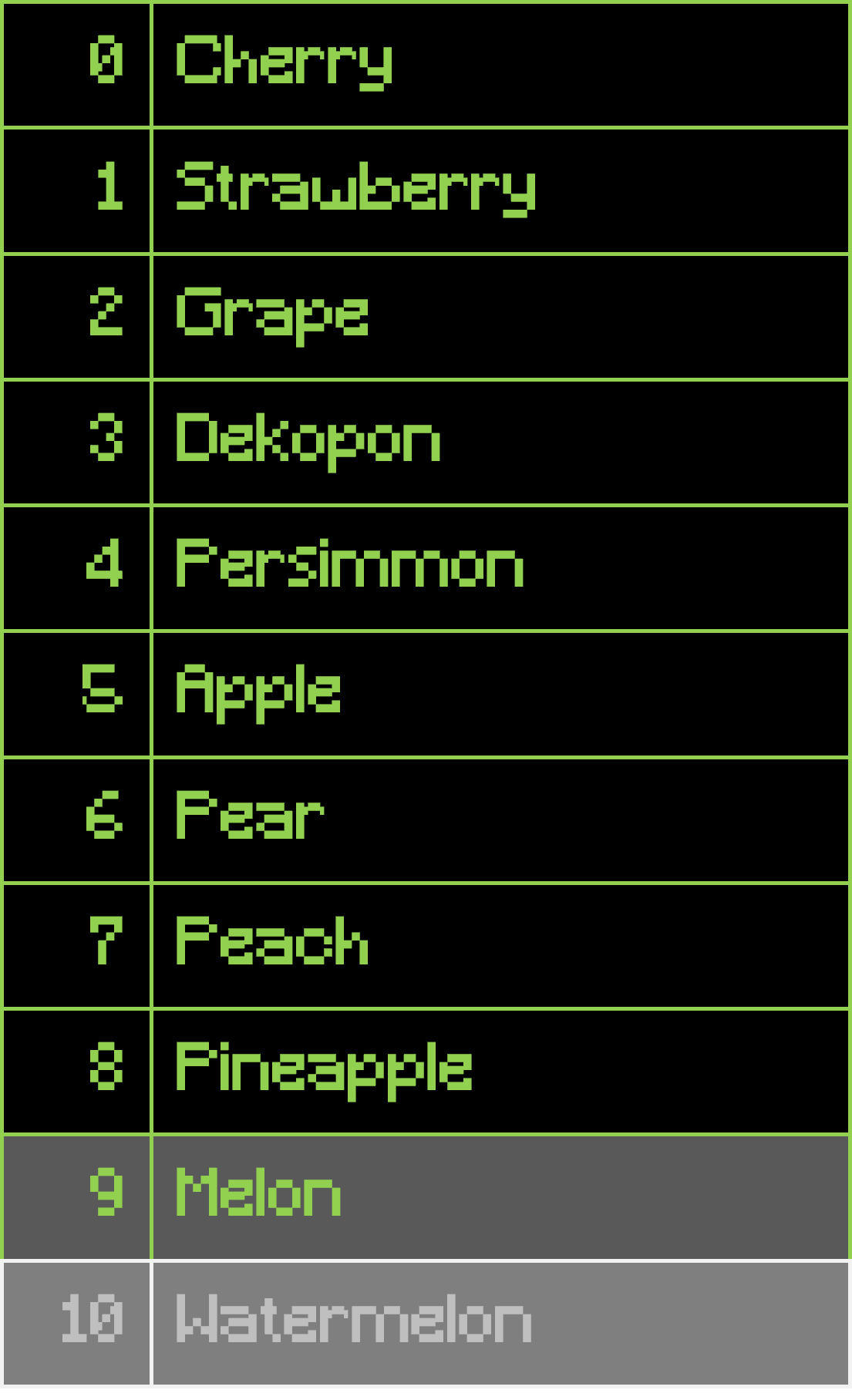
And partition the array:
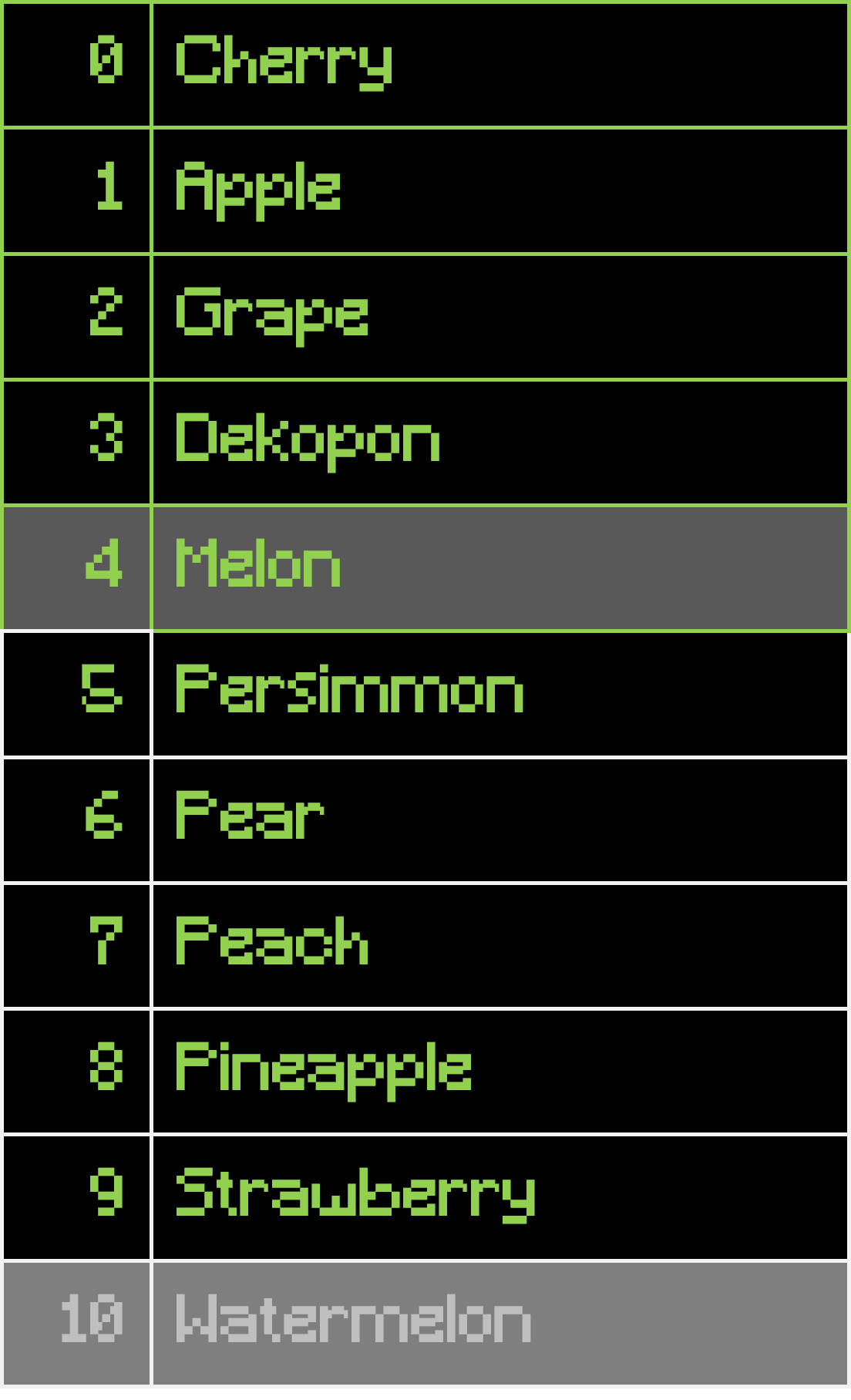
Since the index of the pivot is 4, it must be the 5th smallest element. Thus, we can ignore the elements after it and itself:
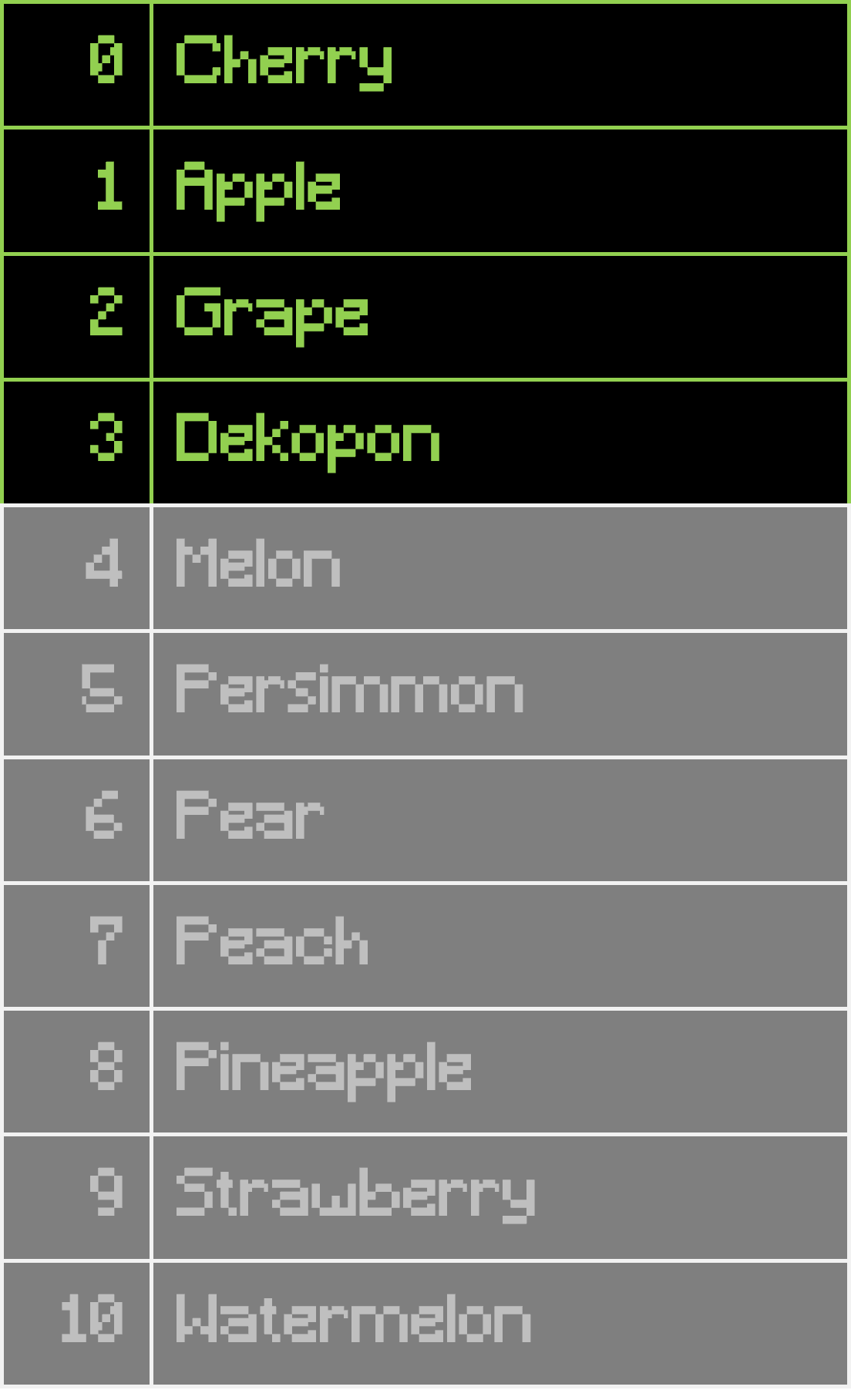
We can continue this process until we find our desired element.
Hint: You can use the function strcmp() to compare the strings.
Input
The first line contains an integer N.
The next N lines contain a string.
The last line contains another integer k.
Output
The kth smallest string in the list.