| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12459 | Sierpinski Carpet |
|
| 14079 | Doraemon and Rubik's Cube ver.2 |
|
Description
This is a Sierpinski Carpet.

The construction of a Sierpinski Carpet is stated as follows. Initially, you are given a white square.
-
Divide the square into nine subsquares in a 3-by-3 grid.
-
Color the center subsquare with black.
-
For the rest eight subsquare, repeat step 1
For example,

Initially (after zero iteration), there is 0 black square in the Sierpinski Carpet.
After one iteration, there is 1 black square in the Sierpinski Carpet.
After two iterations, there are 9 black squares in the Sierpinski Carpet.
After three iterations, there are 73 black squares in the Sierpinski Carpet
Given an integer k, please output number of black squares after k iterations.
Maybe Useless Hint
-
It is suggested to solve this problem using recursion. (Well ... there is mathematic solution, but hope you practice how to design recursion function)
-
Be careful with overflow. Suggest to calculate with long long int.
Input
Input contain a single integer k.
Since there will be overflow issue if k is too big, so in this problem 0 <= k < 10.
Output
Output the number of black squares after the k-th iteration.
Note that there is a newline character after the output.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

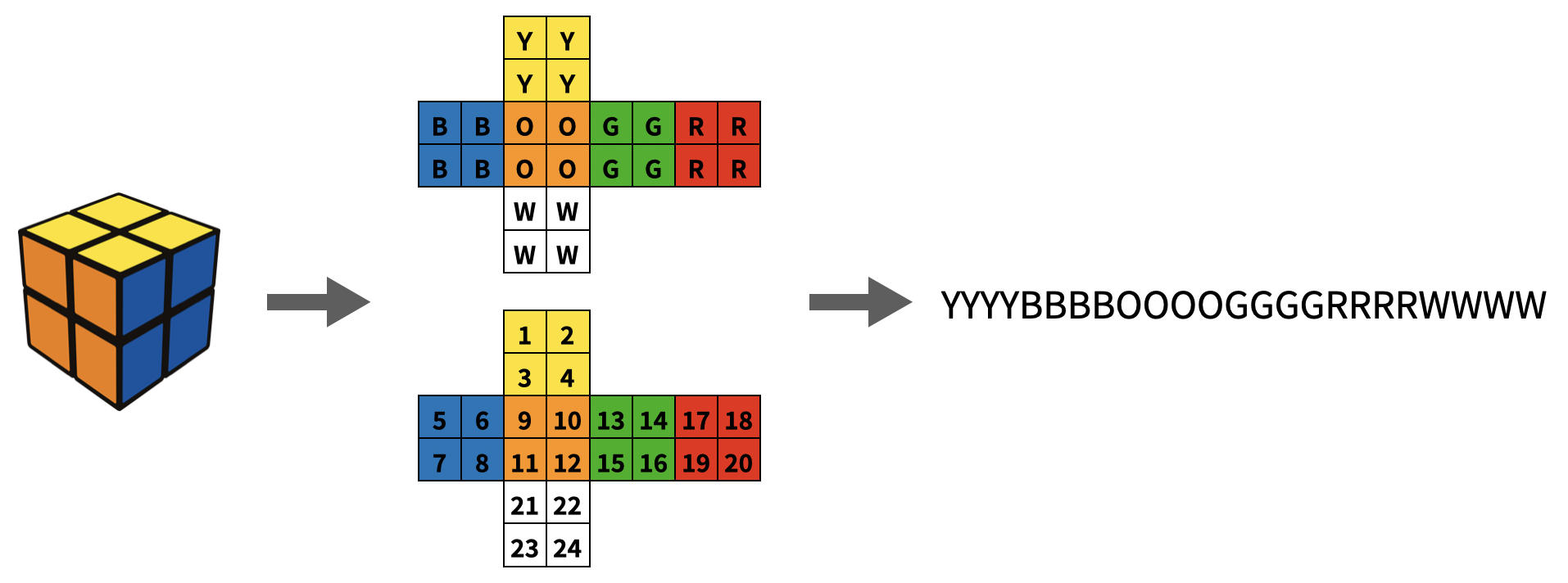
Doraemon enjoys solving the Rubik's Cube.
Today, he received a scrambled 2×2×2 Rubik's Cube and wants to find all the solutions that can be achieved within N moves.
Can you help him out?
To represent the state of a 2x2x2 Rubik's Cube, we use a string consisting of W, O, B, G, Y and R, representing white, orange, blue, green, yellow, and red colors, respectively, and the string has a length of 24. For more details, you can refer to the above image.
We define a move performed on a Rubik's Cube as a clockwise rotation of one of its six faces (Up, Left, Front, Right, Back, Down). To simplify this problem, the counterclockwise rotation is defined as equivalent to performing three moves.
Implementation
In this problem, the code for preprocessing the Rubik's Cube state string, I/O and some useful functions are already provided.
#include <stdio.h>#define UP 0#define LEFT 1#define FRONT 2#define RIGHT 3#define BACK 4#define DOWN 5char rubiks[6][4];char rotateIndex[6][3][4][2] = {{{{0, 0}, {0, 2}, {0, 3}, {0, 1}}, {{1, 0}, {2, 0}, {3, 0}, {4, 0}}, {{1, 1}, {2, 1}, {3, 1}, {4, 1}}},{{{1, 0}, {1, 2}, {1, 3}, {1, 1}}, {{4, 1}, {5, 2}, {2, 2}, {0, 2}}, {{4, 3}, {5, 0}, {2, 0}, {0, 0}}},{{{2, 0}, {2, 2}, {2, 3}, {2, 1}}, {{1, 1}, {5, 0}, {3, 2}, {0, 3}}, {{1, 3}, {5, 1}, {3, 0}, {0, 2}}},{{{3, 0}, {3, 2}, {3, 3}, {3, 1}}, {{2, 1}, {5, 1}, {4, 2}, {0, 1}}, {{2, 3}, {5, 3}, {4, 0}, {0, 3}}},{{{4, 0}, {4, 2}, {4, 3}, {4, 1}}, {{3, 1}, {5, 3}, {1, 2}, {0, 0}}, {{3, 3}, {5, 2}, {1, 0}, {0, 1}}},{{{5, 0}, {5, 2}, {5, 3}, {5, 1}}, {{1, 3}, {4, 3}, {3, 3}, {2, 3}}, {{1, 2}, {4, 2}, {3, 2}, {2, 2}}}};int N;void readRubiksState() { char state[30];scanf("%d %s", &N, state);for (int i=0; i<6; i++) {for (int j=0; j<4; j++) {rubiks[i][j] = state[i * 4 + j];}}}// Pass UP/LEFT/FRONT/RIGHT/BACK/DOWN as parameters to perform the movevoid move(int face) {for (int i=0; i<3; i++) {for (int j=0; j<3; j++) {int ax = rotateIndex[face][i][j][0];int ay = rotateIndex[face][i][j][1];int bx = rotateIndex[face][i][j+1][0];int by = rotateIndex[face][i][j+1][1];char tmp = rubiks[ax][ay];rubiks[ax][ay] = rubiks[bx][by];rubiks[bx][by] = tmp;}}}// Print the Rubik's Cube state for debugging purposesvoid printRubiks() {printf(" %c%c\n %c%c\n", rubiks[0][0], rubiks[0][1], rubiks[0][2], rubiks[0][3]);for (int i=1; i<5; i++) printf("%c%c", rubiks[i][0], rubiks[i][1]);printf("\n");for (int i=1; i<5; i++) printf("%c%c", rubiks[i][2], rubiks[i][3]);printf("\n %c%c\n %c%c\n", rubiks[5][0], rubiks[5][1], rubiks[5][2], rubiks[5][3]);}// Return 1 if the Rubik's Cube is solved, otherwise return 0int isSolved() {char colors[6] = {'W', 'O', 'B', 'G', 'Y', 'R'};int status = 0;for (int i=0; i<6; i++) {for (int j=1; j<4; j++) if (rubiks[i][0] != rubiks[i][j]) return 0;for (int j=0; j<6; j++) {if (colors[j] == rubiks[i][0]) {status |= (1<<j);break;}}}return ((1 << 6) - 1 == status);} // B(Back), D(Down), F(Front), L(Left), R(Right), U(Up)char moveNotation[6] = {'U', 'L', 'F', 'R', 'B', 'D'};int moveOrder[] = {4, 5, 2, 1, 3, 0};int moveSolution[5];// Output all the solutions that can be achieved within n moves using the terms 'B,' 'D,' 'F,' 'L,' 'R,' and 'U' // Please keep in mind that multiple solutions may exist, so please output them in lexicographical ordervoidsolve(int n) {// TODO: utilize move(), printRubiks(), isSolved() to implement the function}int main() { readRubiksState(); solve(N); return 0; }
Your only task is to implement solve(int n) function:
Output all the solutions that can be achieved within n moves using the terms 'B,' 'D,' 'F,' 'L,' 'R,' and 'U'.
Please keep in mind that multiple solutions may exist, so please output them in lexicographical order.
In your implementation, you may need to utilize the following functions:
move(int face): Use UP/LEFT/FRONT/RIGHT/BACK/DOWN as parameters to perform the move.isSolved(): Return 1 if the Rubik's Cube is solved; otherwise, return 0.printRubiks(): Print the Rubik's Cube state for debugging purposes.
There are some declared variables for your convenience:
moveNotation: Use these variables to output the corresponding move notations.moveOrder: Sort the moves by the lexicographical order of their move notations.moveSolution: You can store the solution during your recursion process.
You can trace the code for more detailed information.
Example I/O
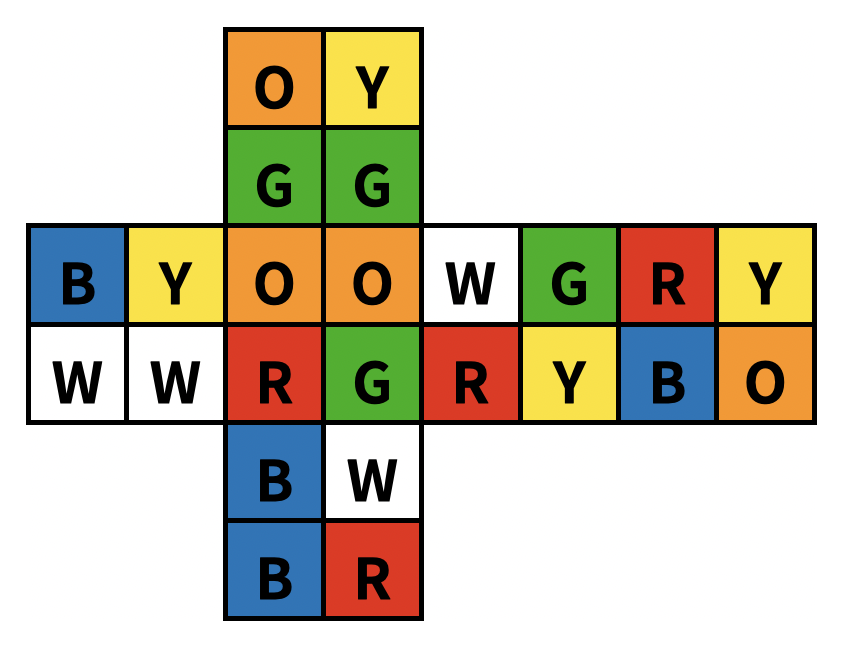
In the sample input, there are 8 ways to solve it within 5 moves:
move(DOWN); move(BACK); move(DOWN);move(DOWN); move(BACK); move(UP);move(DOWN); move(FRONT); move(LEFT);move(DOWN); move(FRONT); move(RIGHT);move(UP); move(LEFT); move(BACK);move(UP); move(LEFT); move(FRONT);move(UP); move(RIGHT); move(DOWN);move(UP); move(RIGHT); move(UP);
Test Case Constraints
- 20% n = 1
- 80% No further constraints
Input
A single line consists of an integer n (1 ≤ n ≤ 5) and a string that represents the state of a Rubik's Cube.
- The string has a length of exactly 24 characters and contains only the characters 'Y', 'B', 'O', 'G', 'R', and 'W'.
- It is guaranteed that the given Rubik's Cube is not in a solved state and is solvable within n moves.
Output
If there are x possible solutions, then please output x lines.
Each line should consist of the solution for the given Rubik's Cube using the terms 'B,' 'D,' 'F,' 'L,' 'R,' and 'U,' and ensure that they are presented in lexicographical order.