| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12486 | Tower of Hanoi |
|
| 14041 | LCM + GCD |
|
Description
The Tower of Hanoi is a mathematical game puzzle. It consists of three rods, which are A, B and C. The puzzle starts with n disks in ascending order of size on rod A, the smallest at the top.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.
Write a program to simulate the optimal moves of the disks. Print the number of disk which is moved in each step.
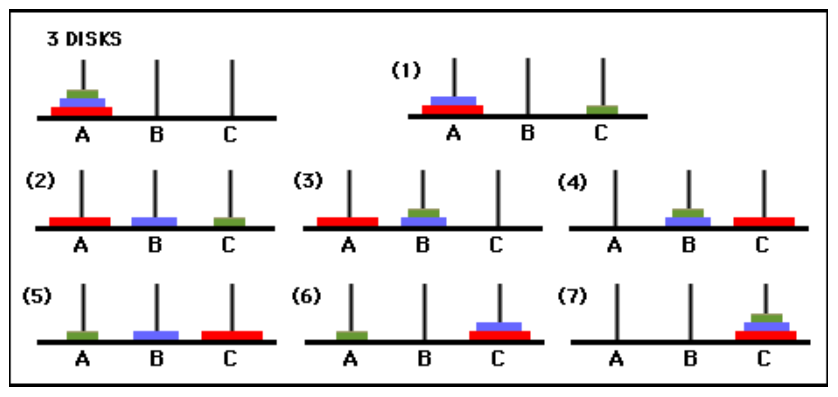
For example, if n = 3, the moves of each steps are:
move disk 1 from rod A to rod C
move disk 2 from rod A to rod B
move disk 1 from rod C to rod B
move disk 3 from rod A to rod C
move disk 1 from rod B to rod A
move disk 2 from rod B to rod C
move disk 1 from rod A to rod C
HINT : You can modify this sample code and implement the function 'hanoi'
#include <stdio.h>
void hanoi(int n, char A, char B, char C);
int main(){
int n;
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
Input
An integer n (0<n<20), which means the number of disk.
Output
Print out the information of each step, and there is a '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Calculate the least common multiple and greatest common divisor of two integers.
Greatest Common Divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers x, y, the greatest common divisor of x and y is denoted 
For example, the GCD of 8 and 12 is 4, that is,
LCM is the short form for “Least Common Multiple.” The least common multiple is defined as the smallest multiple that two or more numbers have in common.
For example: Take two integers, 2 and 3.
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20….
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 ….
6, 12, and 18 are common multiples of 2 and 3. The number 6 is the smallest. Therefore, 6 is the least common multiple of 2 and 3.
Input
Two integers x, y
1 < x, y< 10000
Output
Output the least common multiple and greatest common divisor separated by space.
Don't forget to include '\n'
