| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 10998 | Stack |
|
| 12767 | The One Function and The Power Of Matrix |
|
| 13520 | Dynamic Array |
|
| 13878 | OFfood |
|
Description
A stack is an abstract data type that serves as a collection of elements, where a node can be added to a stack and removed from a stack only at its top. Two principal operations can be used to manipulate a stack: push, which adds an element at the top, and pop, which removes the element at the top of the collection.
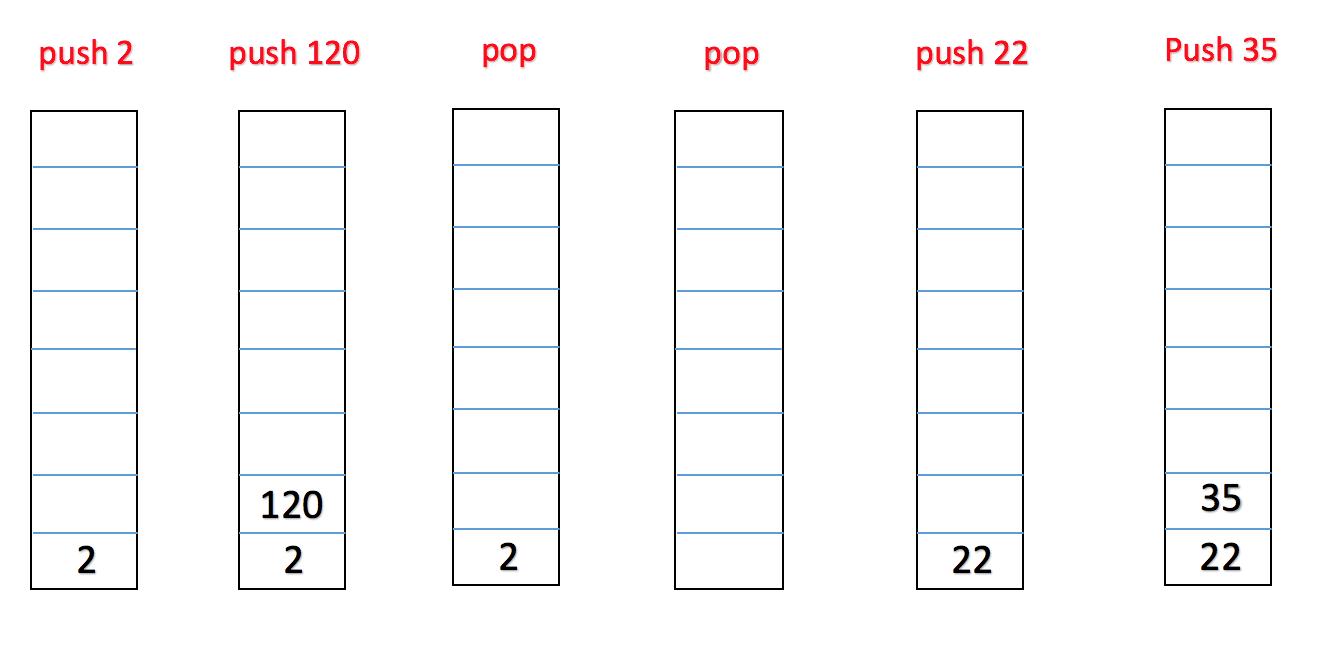
Let’s see how the stack data structure can be realized in C++.We have an approach to implement stack: linked list. Thus, we define a class as follows:
class List_stack {
public:
List_stack();
~List_stack();
void push(const int &);
void pop();
void print();
private:
ListNode *head;
ListNode *tail;
};
where List_stack implements the stack data structure
REQUIREMENTS:
Implement the constructor, destructor, push(), pop() and print() member functions of List_stack classes.
Note:
1.This problem involves three files.
- function.h: Class definitions.
- function.cpp: Member-function definitions.
- main.cpp: A driver program to test your class implementation.
You will be provided with main.cpp and function.h, and asked to implement function.cpp.
function.h
main.cpp
2.For OJ submission:
Step 1. Submit only your function.cpp into the submission block.
Step 2. Check the results and debug your program if necessary.
Input
There are three kinds of commands:
- “push integerA” represents adding an element with int value A at the top of the stack.
- “pop “ represents removing the element at the top of the stack.
- “print” represents showing the current content of the stack.
Each command is followed by a new line character.
Input terminated by EOF.
Output
The output should consist of the current state of the stack.
When the stack is empty, you don’t need to print anything except a new line character.
Sample Input Download
Sample Output Download
Partial Judge Code
10998.cppPartial Judge Header
10998.hTags
Discuss
Description
There is a function called "the one function",
the function is defined as:
F(N, M) = 1, if M <= N,
F(N, M) = F(N, M-1) + F(N, M - 2) + ... + F(N, M - N), if M > N
Given you N, M, tell the result of F(N, M) module 1000000009.
ouo.
Updated at: 2020/05/17 19:00, sorry for the typo in the description.
This is an exercise of operator overloading,
it is recommended that you can follow the partial judge code to finish your work.
There are 8 member functions and 1 additional function that you should implement.
Read the comments carefully to better understand the structure of the partial judge code.
You should choose 'c++11' as the option of submission.
For sample input 1,
N = 3, M = 5,
so F(3, 1) = F(3, 2) = F(3, 3) = 1,
and F(3, 4) = F(3, 3) + F(3, 2) + F(3, 1) = 3
and F(3, 5) = F(3, 4) + F(3, 3) + F(3, 2) = 5
and F(3, 5) % 100000009 = 5,
so the output must be 5.
Input
The input contains 1 line,
the first line contains 2 numbers N, M.
It is guaranteed that:
1 <= N <= 100
1 <= M <= 10^9
Output
The output contains 1 line.
Output the answer of F(N, M), and a newline character at the end of line.
Sample Input Download
Sample Output Download
Partial Judge Code
12767.cppPartial Judge Header
12767.hTags
Discuss
Description
Array vs. Linked List
Array is a basic and fundamental concept in C/C++. It is a series of data which is arranged continiously in the memory space and can be accessed by index. Array is fast for indexing (using the given index to access the certain data), because the memory address of the destination can be calculated quickly. However, the capacity of the array is fixed after the declaration.
In I2PI (introduction of programming 1), we introduce a data structure called "linked list" which supports appending and deleting elements dynamically. The elements are stored in a series of "nodes", where each node points to the address of the next node. It is fast at appending elements but slow at indexing. To access the item of index i, you need to move i steps from head to obtain it.
Dynamic Array
In this problem, we will introduce a new data structure called "dynamic array" (abbreviated to "Darray" in the following statement) which supports dynamic capacity and indexing. We targeted to a simple Darray which has the following three variables
- size : the number of elements stored in the array
- capacity : the maximum number of elements which can be stored in the array
- *data : the pointer which stores the address of the array
and two operations
- pushback: append an element to the back
- indexing : access the data by the given index.
To understand the concept of size and capacity, consider an array declaration:
// or
int *data = new int[5];
At first, the capacity is 5, but the size is 0 because no data is stored inside the array. Next, we push 5 elements to the array:
the capacity is still 5 but the size changes from 0 to 5. Therefore, no element can be appended to the array.
If we still want to append additional elements, we'll allocate a new array space with the double capacity and copy the data from old array to the new one. Note that the old array should be freed to avoid memory leak.
In this case, the capacity becomes 10 and the size is 6.
Implementation
You should implement the following functions based on the description above:
- int& operator[](int): access data like using array. Users and main.cpp should/will not access the index which is greater or equal to size.
- void pushback(int x): append the element x
- void clear(void): clear the array (set size to 0) so that the next pushbacks will place elements in data[0],data[1] and so on.
- int length(void): return the current size.
- void resize(void): double the capacity and copy the data.
- ~Darray(): destructor
Note that main.cpp acts like a functional tester for your Darray. There's no need to understand it. You should test your Darray by yourself.
class Darray {
public:
Darray() {
capacity = 100;
size = 0;
data = new int[capacity];
};
~Darray();
int& operator[](int);
void pushback(int x);
void clear(void);
int length(void);
private:
void resize(void); // double the capacity
int *data;
int capacity;
int size;
};
Darray arr;
for (int i = 0; i < 5; i++) arr.pushback(i*i);
arr[2] += 100 + arr[3];
for (int i = 0; i < arr.length(); i++)
cout << arr[2] << ' '; // Print: 0 1 113 9 16
cout << endl << arr.length() << endl; // Print: 5
arr.clear();
cout << arr.length() << endl; // Print: 0
arr.pushback(9487);
cout << arr.length() << ' ' << arr[0] << endl; // Print: 1 9487
More Notes: Time Complexity of Dynamic Array
Although it seems that copying the whole array will make dynamic array slow, we will analyze the time complexity to show that dynamic array is fast. Recall what Big-O Notation is where we introduced it in "The Josephus problem". O(2n+100)=O(2n)=O(n) means that the operation takes about n steps while O(2)=O(1) takes "constant" time. For array operations, we wish to have O(1) of indexing and pushback. In the following analysis, we will evaluate the amortized time complexity, which can be comprehended as calculating the average time complexity instead of the complexity of total operations. Amortized time complexity = (complexity of total operations) / (number of operations).
Suppose that C0 is the initial capacity and n is the number of operation of pushback. We discuss the time complexity in several cases:
- Expand 0 time, n <= C0.
Since there's no expand operation, the total time complexity is O(1)*n=O(n). The amortized time complexity is O(n)/n=O(1). - Expand 1 time, C0 < n <= C1, C1 = 2*C0.
Push C0 items to array: O(C0)
Expand and copy: O(C0), since there're C0 elements to be copied.
Push n-C0 items to array: O(n-C0)
The total time complexity is O(C0)+O(C0)+O(n-C0) = O(n+C0). Since C0 < n <= C1, O(2C0) < total time complexity <= O(3C0). The amortized time complexity ranges in [O(3/2), O(2)). We identify it by the upper bound : O(2). - Expand 2 times, C1 < n <= C2, C2 = 2*C1.
The amortized time complexity should be O(3). You can verify it by your own.
From the above analysis, if it expand i times, the amortized time complexity for appending an element is O(i+1). However, i won't be very large because the capacity grows exponentially so that we often regard the complexity as O(1), or, constant time. For instance, C0=100, after expanding 20 times, the capacity will be 100*220≈108.
Input
This is handled by the main function.
Output
This is handled by the main function.
Sample Input Download
Sample Output Download
Partial Judge Code
13520.cppPartial Judge Header
13520.hTags
Discuss
Description
MM, a slashie, is an expert in many different realms. One of his skills is having great creation.
Today, he comes up with a good idea for an app, called ‘OFfood’.
‘OFfood’ is an abbreviation of ‘on-floor food’(在地美食). It is an app recording information about on-floor food. Users can report the on-floor food they see or check where are the on-floor foods and their condition. In particular, there is some information for the food: type, name, fly, and position.
- type: There are only 2 types of food: fruit and meat.
- name: Each food has its unique name, which is a string containing only English letters.
- fly: There would be some flies on the food. For the food on the floor, the flies would add by 4 every 5 minutes for fruit, and add by 5 every 5 minutes for meat.
- position: The position would only be either floor, stomach, or trash can.
There are 4 types of operations that users may perform:
- report n k: The user report that they see an on-floor food, which its name is n and the type is k, with no fly.
- eat n k: Someone eats the food on the floor with name n, type k. The food n then changes its position to ‘stomach’.
- throw n k: Someone throws the food on the floor with name n and type k, into the trash can. The food n then changes its position into ‘trashcan’.
- mix n m k1 k2: Someone mix the food with name n, type k1 with the food with name m, type k2. The food m still remains its condition, while the food n is mixed with food m and its type remains the same. The mixed food would have a new name s, which s is the concatenate of m and n. The amount of flies is the sum of the fly of the two food. It is guaranteed that the two foods are on the floor when mixed.
MM now collects the operations that users made. He wants to know some information about the foods:
- How many people are sick because they eat rotten food. People would definitely get sick if they ate rotten food. The fruit is rotten if they have more than(>=) 10 flies on it, and the meat is rotten if they have more than(>=) 20 flies on it. What's more, each rotten food would surely be eaten by different people since people who eat rotten food would be sent to the hospital immediately.
- How much food is still on the floor.
- The food’s name list, sorted by lexicographical order, which the food is still on the floor.
Since you are a code farmer(碼農), help him to collect the data he wants.
You only have to finish the function defined in the header file.
Input
The first line contains an integer t, which means MM collects the information for 5 * t minutes.
Then, there are t parts of operations, each part is separated by 5 minutes intervals.
For every part, the first line contains an integer n, representing the number of operations in this part.
The following n lines, each represent an operation, following the format in the description.
Constrains:
1 <= t <= 40
1 <= n <= 10
number of fruit <= 100
number of meat <= 100
Output
The first line contains an integer, representing the number of sick people.
The second line contains an integer, representing the amount of food still on the floor.
The following n lines, each contain a string, representing a food’s name. The foods are sorted by lexicographical order.