| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 10990 | cheat sheet |
|
| 13848 | Intertwined syntax forest |
|
| 13852 | Reconstruct BSTs with swapped paternity |
|
| 13864 | Moving the books |
|
Description
Linked list
typedef struct _Node {
int data;
struct _Node *next;
} Node;
/* print the content of the linked list.*/
void printList(Node *head)
{
Node *temp;
for(temp=head; temp!=NULL; temp=temp->next) {
printf("%d ", temp->data);
}
}
/*Insert a node after the node pointed by nd.
Return 1 if insertion succeeds.
Otherwise, return 0.*/
int insertNode(Node* nd, int data)
{
if (nd != NULL) {
Node* temp = (Node*)malloc(sizeof(Node));
temp->data = data;
temp->next = nd->next;
nd->next = temp;
return 1;
}
return 0;
}
/*Delete a node after the node pointed by nd.
Return 1 if insertion succeeds.
Otherwise, return 0.*/
int deleteNode(Node* nd)
{
if (nd != NULL) {
Node* temp = nd->next;
if (temp != NULL) {
nd -> next = temp->next;
free(temp);
return 1;
}
}
return 0;
}
Binary tree
typedef struct _node {
int data;
struct _node *left, *right;
} BTNode;
Tree traversal
- Pre-order: visit root, left subtree, and right subtree
- In-order: visit left subtree, root, and right subtree
- Post-order: visit left subtree, right subtree, and root
Expression order
- Prefix: operator, left operand,and right operand
- Infix: left operand, operator, and right operand
- Postfix: left operand, right operand, and operator
Syntax tree
The internal nodes are operators, and the leaves are operands.
Recursive evaluation of prefix expression
/*It is a pseudo code */
int evalBoolExpr(){
char c = getchar();
If c is an operator
op1 = evalBoolExpr();
op2 = evalBoolExpr();
return op1 c op2;
Else if c is a variable
return the value of c;
}
Grammar of infix expression with parenthesis
- EXPR = FACTOR| EXPR OP FACTOR
- FACTROR = ID | (EXPR)
/*Suppose expr[] is an array of expression and pos is the current position, which initially is strlen(expr)-1. */
/*-------------------------------------*/
BTNode* makeNode(char c)
{
int i;
BTNode *node = (BTNode*)malloc(sizeof(BTNode));
set node->data
node->left = NULL;
node->right = NULL;
return node;
}
/*-------------------------------------*/
BTNode* FACTOR()
{
char c;
BTNode *node = NULL;
if (pos>=0) {
c = expr[pos--];
if (c is an ID) {
node = makeNode(c);
} else if (c==‘)’) {
node = EXPR();
if(expr[pos--]!= '(') {
printf("Error!\n");
freeTree(node);
}
}
}
return node;
}
/*-------------------------------------*/
BTNode* EXPR()
{
char c;
BTNode *node = NULL, *right=NULL;
if (pos>=0) {
node = right = FACTOR();
if (pos>0) {
c = expr[pos];
if (c is an operator) {
node = makeNode(c);
node->right = right;
pos--;
node->left = EXPR();
}
}
}
return node;
}
Input
Output
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given several prefix expressions, each represents a function. The expression has at most 4 types of operations and 5 variables, described below.
We explain the 4 operations using infix:
1. Addition. 'a+b' means a plus b, in which a, b are integers.
2. Negation. '-a' means a*(-1), in which a is an integer.
3. Multiplication. 'a*b' means a times b, in which a, b are integers.
4. Function call. 'f@a' means return the value f(a), in which f is a function and a is an integer.
For variables, they are all integers, and the 5 variables are A, B, C, D, and X, respectively. For A, B, C, and D, you will get their values from input. For X, it is the parameter that you gave the function.
The function name will be a lowercase letter. Given the function name and the prefix expression of each function. Now here are q queries: Given the function name and the parameter for the function, and the value of A, B, C, and D, please output the calculation result.
For sample input 2, here are the syntax trees for the 4 functions.
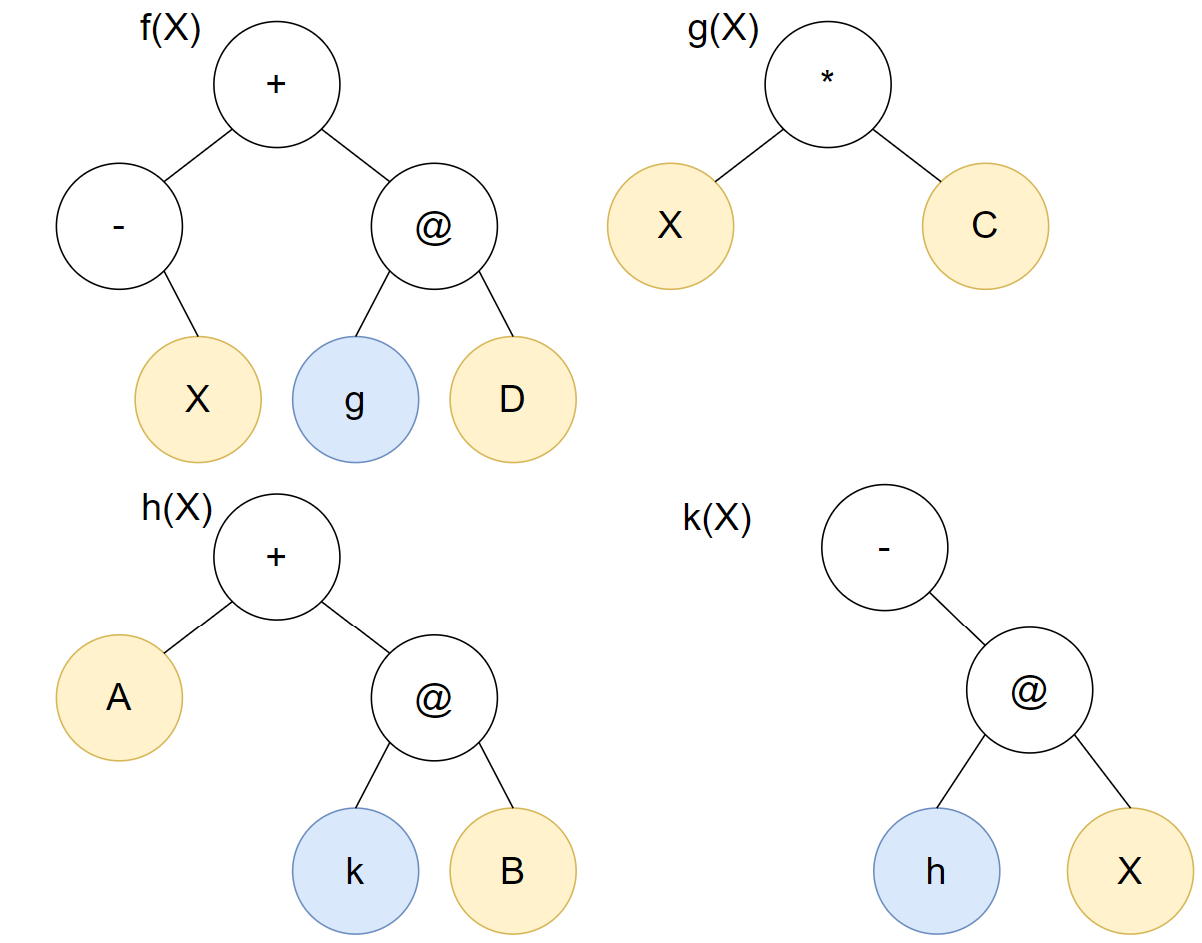
Note the parameter X for the functions are different. For example, it's 1 for f and it's 5 for g, in the second query.
For the second type operation, negation, it has only one child in the syntax tree, which is the right child.
In this problem, calling functions often cause an error since the calculation process may not stop because of repeating calling the same functions. For example, the first query in sample input 2 would call function h first, then the function h would call function k. Function k would then call function h, and never ends. In this case, you should stop the process and print 'Error'.
Input
The first line contains two integers, n and q, which means there are n functions and q queries.
The following n lines each contain a lowercase letter representing the function name, and a string representing the prefix expression, separated by space.
The last q lines each contain a lowercase letter and five integers, separated by spaces, each representing the function name, the parameter X, A, B, C, and D.
Constraints:
1 ≤ n ≤ 26
1 ≤ q ≤ 100
-1000 ≤ A, B, C, D, X ≤ 1000
The expression would not contain over 200 characters.
For cases 1~4, it is guaranteed that no error occurs during process, and no negation operation.
For cases 5~8, it is guaranteed that no error occurs during process.
For other cases, no further constraints.
Output
An integer represents the calculation result. Since the answer could be large, please output the answer modulo 998244353.
Note
Since the answer should modulo 998244353, you should take the remainder after every operation. Since the result of taking the remainder must be non-negative, the result should add 998244353 if it is negative after modulo. Be free to use the following function:
num %= 998244353;
if(num < 0) num += 998244353;
return num;
}
Sample Input Download
Sample Output Download
Tags
Discuss
Description
What is a Binary Search Tree?
A binary search tree (BST) is a binary tree data structure with the following properties:
- Each node in the tree has at most two child nodes (binary tree).
- For any node, its value is greater than or equal to the values stored in the left subtree.
- For any node, its value is smaller than the values stored in the right subtree.
- For any node, the left subtree and the right subtree are binary search trees respectively as well.
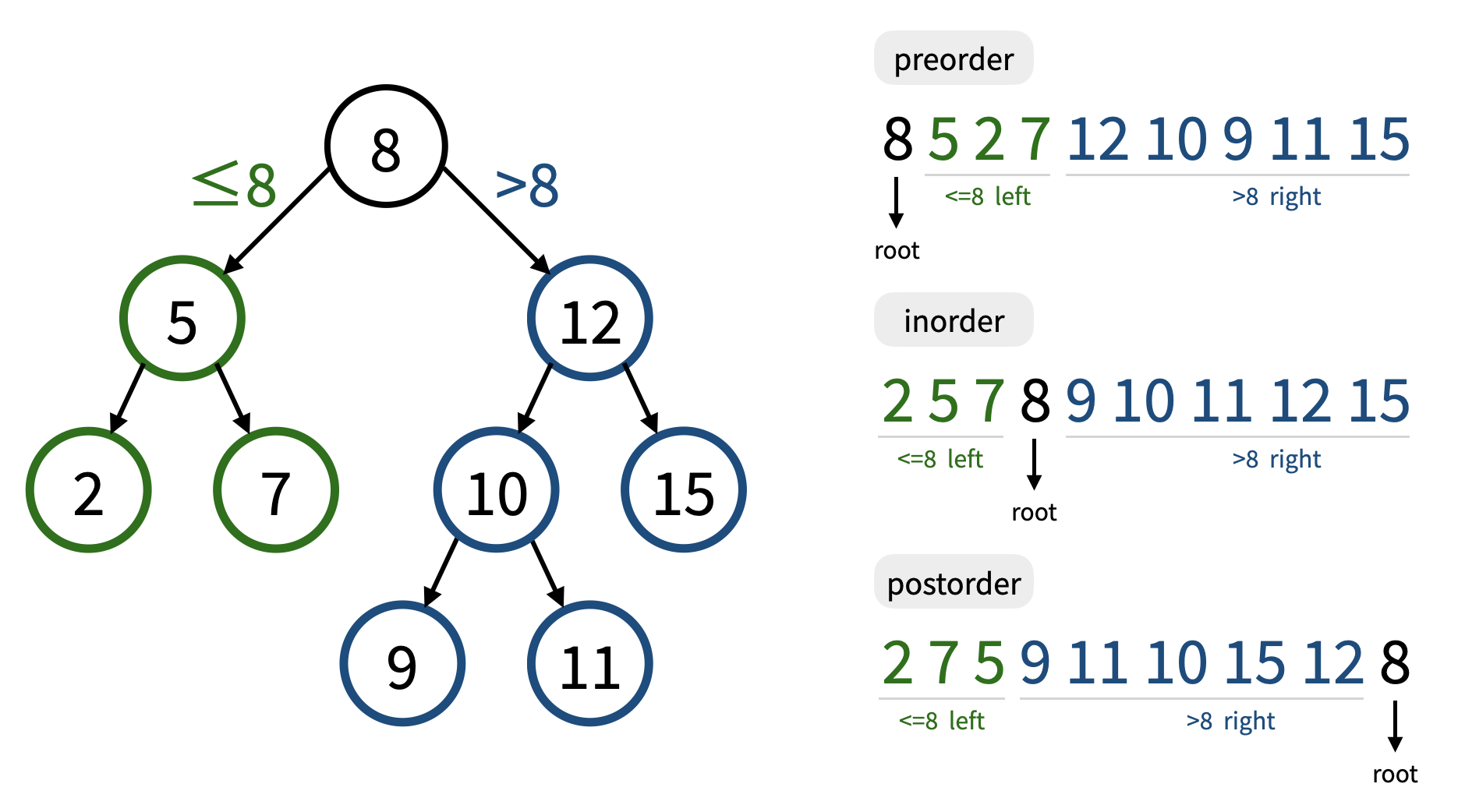
We know that the preorder traversal is based on the order "root -> left subtree -> right subtree". Therefore, for the preorder traversal sequence of a binary search tree, we can observe that the first number is the root of the tree, and in the following sequence, numbers smaller than or equal to the root belong to the left subtree (green part), while numbers larger than the root belong to the right subtree (blue part).
In this problem:
You are given the preorder and inorder sequences of a scrambled binary search tree with unique node values, where we would choose several internal nodes of the original tree and swap each of these nodes with its left or right child.
Please note that in this problem, we guarantee that every non-leaf node has two children, but we do not guarantee that the tree is a perfect binary tree. Besides, we guarantee that no two swapped pairs overlap (that is, contain a same node). In the following image, each color represents a node pair that has been swapped.
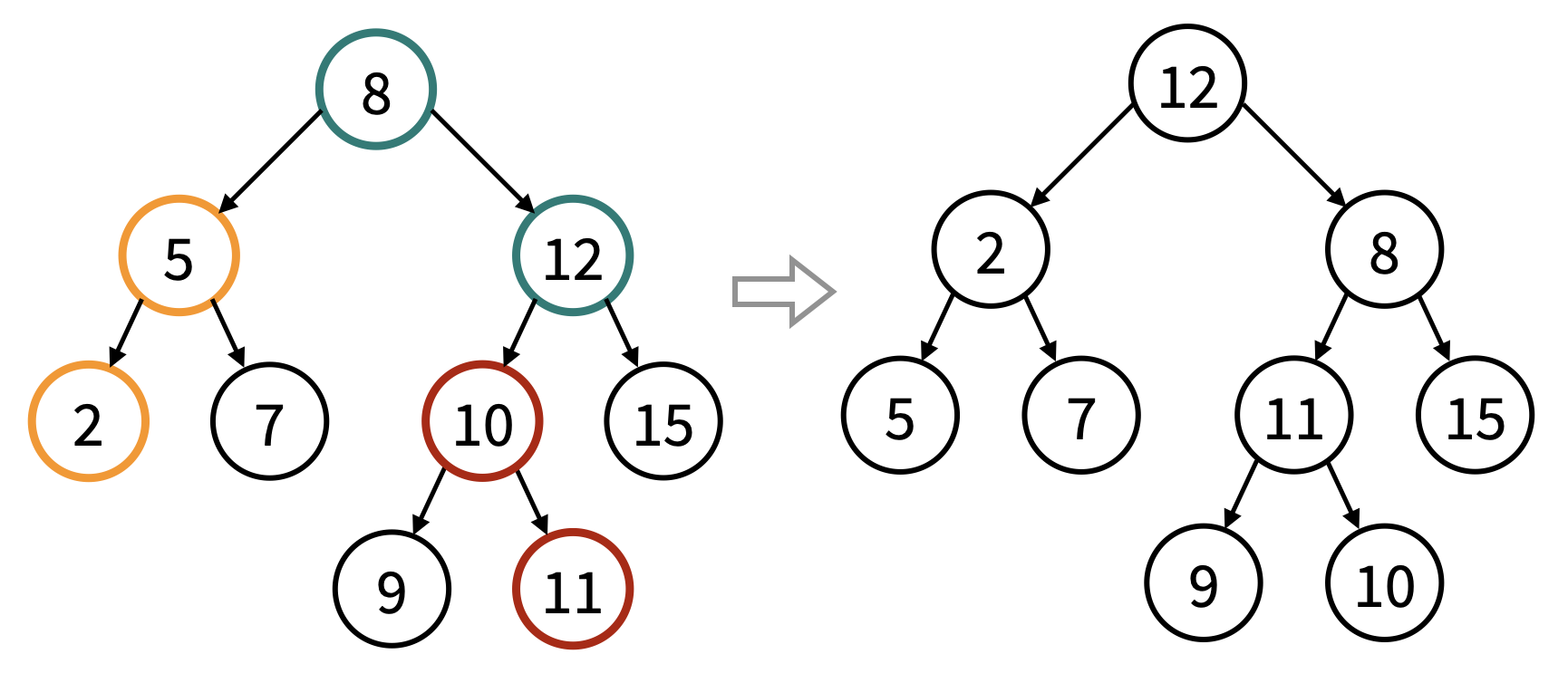
Can you help us reconstruct the original binary search tree and output its postorder sequence?
Input
- The first line contains an integer N (1 ≤ N ≤ 103) - the length of the preorder and the inorder sequences for the scrambled binary search tree.
- The second line contains N integers x1, x2, ..., xN (1 ≤ xi ≤ 105) - representing the preorder sequence.
- The third line contains N integers y1, y2, ..., yN (1 ≤ yi ≤ 105) - representing the inorder sequence.
Test case constraints
- Testcases 1-2: The given tree is a perfect binary tree (see the definition in 13846), and no swapping operations have been applied.
- Testcases 3-4: No swapping operations have been applied.
- Testcases 5-6: The given tree is a perfect binary tree, and for each operation, the chosen node can only be swapped with its left child.
- Testcases 7-8: For each operation, the chosen node can only be swapped with its left child.
- Testcases 9-10: No further constraints.
Hints
- To pass Testcases 1-4, the tree construction method similar to that in 13846 can be applied based solely on the preorder sequence.
- To pass Testcases 5-8, the tree construction method similar to that in 13846 can be applied based solely on the preorder sequence. And, you know where the left child of the current subtree's root is located. See if they have been swapped.
- To pass Testcases 9-10, you should use both the preorder and the inorder sequences.
Output
Output one line that contains N integers - representing the postorder sequence of the original binary search tree. Remember to print '\n' at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The problem is to parse a series of commands to move the books that lie on the table. Initially there are n books lying on their own table (numbered from 0 to n-1, means book 0 lies on table 0) with book bi adjacent to book bi+1 for all 0 <= i < n-1
as shown in the diagram below:
|
Book 0 |
Book 1 |
Book 2 |
Book 3 |
Book 4 |
Book 5 |
…… |
Book N-1 |
|
Table 0 |
Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
Table N-1 |
The valid commands and limited for moving books are:
Any command in which A = B or in which A and B are in the same stack of books is an illegal command. All illegal commands should be ignored and should have no affect on the configuration of books.
1. pile A onto B
Return any books that are stacked on the top of book B to their own table.
Then puts book A and all books on the top of book A onto the top of book B.
2. exit
Finish moving the books
Hint: you can use following code.
version 1:
#include <stdio.h>
#include <stdlib.h>
typedef struct _Node{
struct _Node* next;
int val;
} Node;
Node* table[25];
int pos[25];
void resetBook(int p2) {
// TODO 1
}
void pileOnto(int p1, int p2) {
// TODO 2
}
void initialize(int n) {
for(int i = 0; i<n; i++){
table[i] = (Node*)malloc(sizeof(Node));
table[i]->val = -1;
table[i]->next = (Node*)malloc(sizeof(Node));
table[i]->next->val = i;
pos[i] = i;
table[i]->next->next = NULL;
}
}
int main() {
int n;
scanf("%d", &n);
initialize(n);
while(1){
char input[100] = {0};
int p1, p2; scanf("%s", input);
if(input[0] == 'e') break;
scanf("%d%s%d", &p1, input, &p2);
if(pos[p1] == pos[p2]) continue;
resetBook(p2);
pileOnto(p1, p2);
}
Node* tmp;
for(int i = 0; i < n; i++){
printf("%d:", i);
tmp = table[i]->next;
while(tmp){
printf(" %d", tmp->val);
tmp = tmp->next;
}
printf("\n");
}
return 0;
}
version 2:
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
typedef struct node{
int data;
int table;
struct node *next;
}Node;
Node* nodes[10000];
void clean(int b){
// TODO 1
}
void mymove(int a, int b){
// TODO 2
}
Node* createNode(int data){
Node* node = (Node*)malloc(sizeof(Node));
node->data = data;
node->next = NULL;
node->table = data;
return node;
}
void print(int n){
for (int i = 0; i < n ; i++){
printf("%d:", i);
Node *p = nodes[i];
if (p->table == i){
while(p!= NULL){
printf(" %d", p->data);
p = p->next;
}
}
printf("%c",'\n');
}
}
int main()
{
int n;
char op1[5], op2[5];
int a, b;
scanf("%d", &n);
for (int i = 0; i < n ; i++){
nodes[i] = createNode(i);
}
while(scanf("%s", op1) && op1[0] != 'e'){
scanf("%d %s %d", &a, op2, &b);
if (a == b || nodes[a]->table == nodes[b]->table) continue;
// op1 == "pile", op2 == "onto"
clean(b);
mymove(a, b);
}
print(n);
return 0;
}
Input
The input begins with an integer n on a line by itself representing the number of books in the book world. You may assume that 0 < n < 25.
The number of books is followed by a sequence of book commands, one command per line. Your program should process all commands until the exit command is encountered.
You may assume that all commands will be of the form specified above. There will be no syntactically incorrect commands.
Output
The output should consist of the final state of the books. Each table numbered i (0 <= i < n, where n is the number equal to books initial position) should appear followed immediately by a colon.
If there is at least a book on it, the colon must be followed by one space, followed by a list of books that appear stacked in that position with each book number separated from other book numbers by a space. Don't put any trailing spaces on a line.
There should be one line of output for each book position (i.e., n lines of output where n is the integer on the first line of input).
You are asked to add a new line character at the end.