| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13845 | Syntax forest |
|
| 10966 | Infix to syntax tree |
|
Description
Given several prefix expressions, each representing a function. Such an expression has at most 4 types of operations and 5 variables, described below.
We explain the 4 types of operations using infix:
- Addition. ‘a+b’ means a plus b, in which a, b are integers.
- Subtraction. ‘a-b’ means a minus b, in which a, b are integers.
- Multiplication. ‘a*b’ means a times b, in which a, b are integers.
- Function call. ‘f@a’ means return the value f(a), in which f is a function and a is an integer.
For variables, they are all integers, and the 5 variables are A, B, C, D, and X, respectively. For A, B, C, and D, you will get their values from input. For X, it is the parameter that you gave the function.
The function name will be a lowercase letter. Given the function name and the prefix expression of each function. Now here are q queries: given the function name and the parameter (i.e., X) for the function, and the values of A, B, C, and D, please output the calculation result.
For sample input 2, here are the syntax trees for the 2 functions.
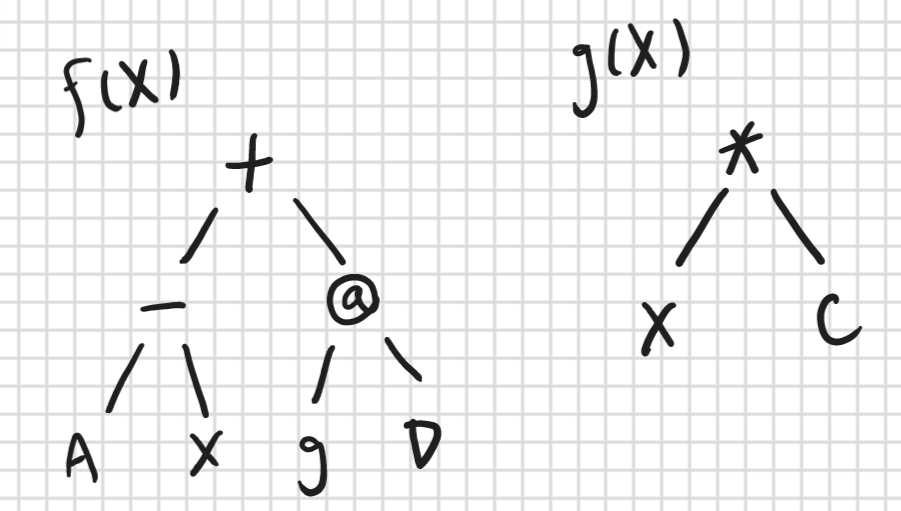
Note the parameter X for the functions are different. For example, in the second query, it’s 1 for f and it’s 5 for g.
Input
The first line contains two integers, n and q, which means there are n functions and q queries.
Each of the following n lines contains a lowercase letter representing the function name, and a string representing the prefix expression, separated by a space.
Each of the last q lines contains a lowercase letter and five integers, separated by spaces, representing the function name, the parameters X, A, B, C, and D, respectively.
Constraints:
1 ≤ n ≤ 26
1 ≤ q ≤ 100
-1000 ≤ A, B, C, D, X ≤ 1000
The expression would not contain over 200 characters.
For cases 1~3, the expressions only contain the first 3 operations.
For other cases, no further constraints.
Output
An integer that represents the calculation result. Since the answer could be large, please output the answer modulo 998244353. After modulo, the answer should be between 0 ~ 998244352.
Note
Since the answer should modulo 998244353, you should take the remainder after every operation (including returning the value of a single variable). Since the result of taking the remainder must be non-negative, the result should add 998244353 if it is negative after modulo. Be free to use the following function:
num %= 998244353;
if(num < 0) num += 998244353;
return num;
}
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given an infix Boolean expression with parentheses, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. Build a corresponding syntax tree for it.
To parse the infix expression with parentheses, use the grammar below.
EXPR = FACTOR | EXPR OP FACTOR
FACTOR = ID | (EXPR)
EXPR is the expression, ID is one of ‘A’, ‘B’, ’C’, or ‘D’, and OP is one of ‘&’ or ‘|’.
You will be provided with main.c and function.h. main.c contains the implementation of functions printPrefix and freeTree. function.h contains the definition of tree node and variables. You only need to implement the following three functions in function.c.
BTNode* makeNode(char c) // create a node without any child
BTNode* EXPR() // parse an infix expression and generate a syntax tree
BTNode* FACTOR() // use the parse grammar FACTOR = ID | (EXPR) to deal with parentheses
For OJ submission:
Step 1. Submit only your function.c into the submission block.(Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
The input contains N infix expressions, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, two operators ‘&’ and ‘|’, and parentheses. All parentheses are matched.
Output
The output contains N prefix expressions without parentheses, which are preorders of syntax trees.