| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11840 | Moving books |
|
| 12183 | Fairy Testing |
|
| 13149 | Ternary Expression Evaluation |
|
| 13845 | Syntax forest |
|
| 13846 | Reconstruct swapped binary search trees |
|
| 13847 | Reconstruct broken binary trees |
|
Description
The problem is to parse a series of commands to move the books that lie on the table. Initially there are n books lying on their own table (numbered from 0 to n-1, means book 0 lies on table 0) with book bi adjacent to book bi+1 for all 0 <= i < n-1
as shown in the diagram below:
|
Book 0 |
Book 1 |
Book 2 |
Book 3 |
Book 4 |
Book 5 |
…… |
Book N-1 |
|
Table 0 |
Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
Table N-1 |
The valid commands and limited for moving books are:
Any command in which A = B or in which A and B are in the same stack of books is an illegal command. All illegal commands should be ignored and should have no affect on the configuration of books.
- move A onto B
Return any books that are stacked on the top of book A and book B to their own table. Then puts book A onto book B.
- move A over B
Return any books that are stacked on the top of book A to their own table.
Then puts book A onto the top of book B.
- pile A onto B
Return any books that are stacked on the top of book B to their own table.
Then puts book A and all books on the top of book A onto the top of book B.
- pile A over B
Put book A and all books on the top of book A onto the top of book B.
- exit
Finish moving the books
Input
The input begins with an integer n on a line by itself representing the number of books in the book world. You may assume that 0 < n < 25.
The number of books is followed by a sequence of book commands, one command per line. Your program should process all commands until the exit command is encountered.
You may assume that all commands will be of the form specified above. There will be no syntactically incorrect commands.
Output
The output should consist of the final state of the books. Each table numbered i (0 <= i < n, where n is the number equal to books initial position) should appear followed immediately by a colon.
If there is at least a book on it, the colon must be followed by one space, followed by a list of books that appear stacked in that position with each book number separated from other book numbers by a space. Don't put any trailing spaces on a line.
There should be one line of output for each book position (i.e., n lines of output where n is the integer on the first line of input).
You are asked to add a new line character at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In this problem, you are given a prefix Boolean expression, which has at most N=10^5 variables and 2 kinds of operators ‘&’ and ‘|’. Each variable has an ID number. The values of these variables can be either 0 or 1, and are all initialized as 0.
You will be given M ID numbers. For each ID number, you should flip (0 will become 1, 1 will become 0) the value of the corresponding variable and then compute/output the result of the prefix Boolean expression.
Example:
Assume the prefix Boolean expression is &[1][2] and the given ID numbers are “2 1”. First the value of variable 2 will change from 0 to 1. The output of &[1][2] is 0&1=0. Next, the value of variable 1 will change from 0 to 1. The output of &[1][2] is 1&1=1.
Hint: (You can go to the Input/Output description directly, and come back for hints if necessary.)
Hint 1: To solve this problem, you can parse the input and derive the output recursively each time a variable is flipped. Unfortunately, this brute-force approach is not efficient and can lead to TLE, in particular the 3rd and 4th testcases in this problem. We encourage you to use the syntax tree of the prefix Boolean expression for better efficiency.
Hint 2: The key idea behind the syntax-tree approach is to avoid re-evaluation of the whole expression every time a bit is flipped. Some more hints are provided for you as follows:
- [Data structure] Use a tree node pointer array to record the address of each variable (leaf) node of the syntax tree: you can locate each variable to be flipped directly;
- [Data structure] For each tree node i, record the value of its subtree (rooted at node i);
- [Algorithm] Starting from the variable node to be flipped, move upward following the syntax tree and update the node values until the output of the syntax tree (or the Boolean expression) can be determined.
Example:
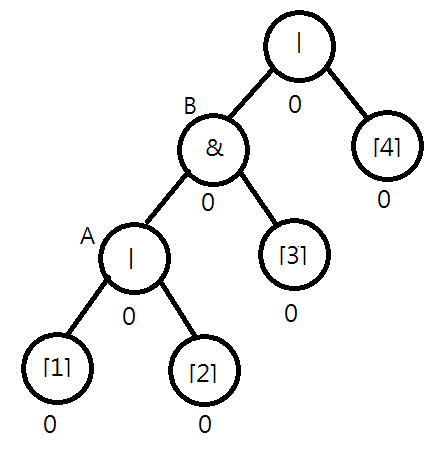
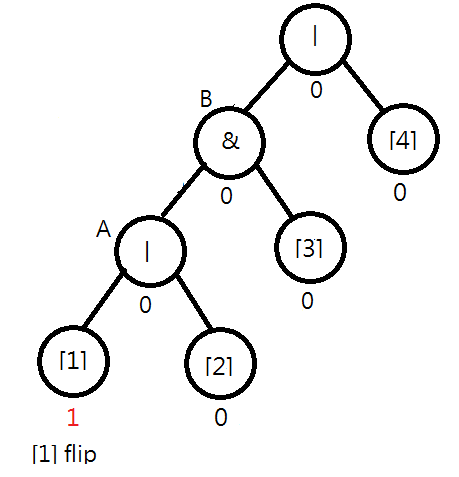
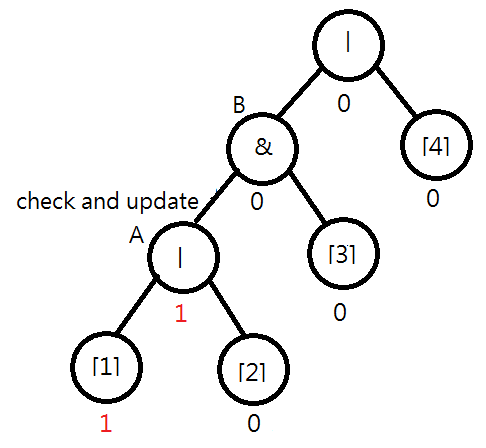
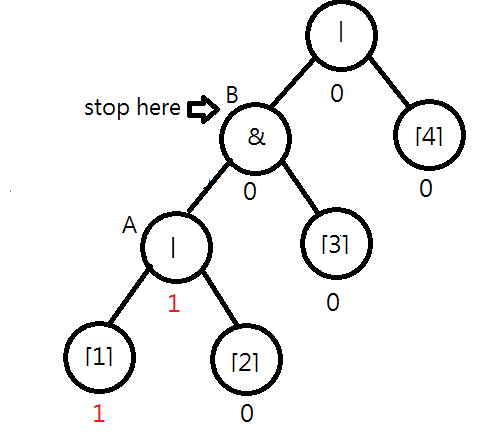
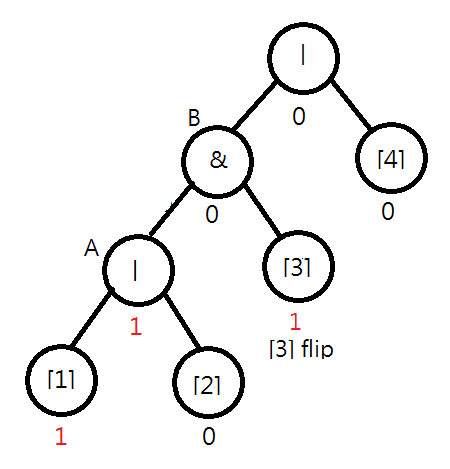
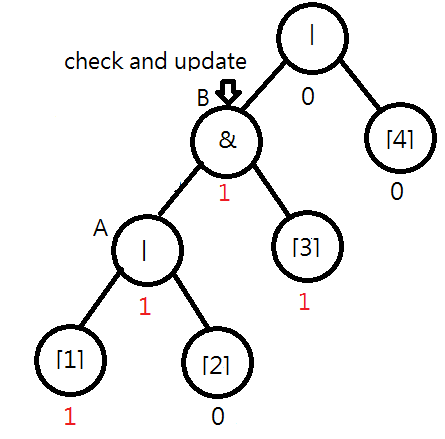
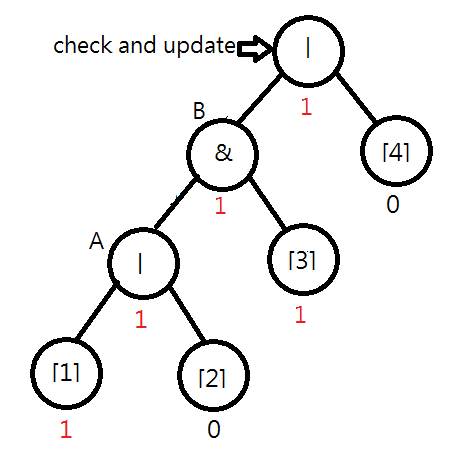
Consider the following syntax tree for "|&|[1][2][3][4]". Assume [1] is flipped. You will find that the value of node A should be changed to 1|0=1. Moreover, you note that the value of B remains unchanged, i.e., 1&0=0, and the checking process can stop.
Later, when [3] is flipped, both the values of node B and the root node should be changed. In this case, the output is also changed.
Sample structure:
typedef struct node{
int value; // This is the value of the subtree, not the ID number
int tokentype;
struct node *leftchild;
struct node *rightchild;
struct node *parent; //pointing to the parent node
}Node;
Node* variable[100001]; // This array stores the pointers pointing to the tree nodes. For example, variable[0] points to the node with ID number 0.
Input
The first line has one number T, 0<T<= 7, indicating the number of testcases.
The following lines are the inputs of the testcases.
Each testcase contains three lines:
1. N, M (0<N<=100000, indicating the number of variables in a given prefix Boolean expression. 0<M<=100000, indicating how many times the values are flipped).
2. A string S, describing the prefix Boolean expression (& means and gate, | means or gate, [i] means a variable ID)
3. M numbers, where each number i means the value of variable i is flipped. The order matters.
Note that all the variables are initially 0.
Each ID number only appears once in the prefix Boolean expression.
The depth of the tree is no more than 30.
Output
For each testcase, you should output M lines, each showing the output of the prefix Boolean expression after a variable is flipped.
0 for false, 1 for true.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The ternary operator is an operator in C. Its syntax is as follows:
It is often used to replace a simple if-else statement such as:
You can also combine several ternary operators together such as:
Now you are given a ternary expression, in which all the values are either true or false. Next you must evaluate the ternary expression with different combinations of values.
More specifically, a valid ternary expression is either:
or
And the evaluation order of a ternary expression can be explained as follows:
- If the valid ternary expression is a single value, then just return the value.
- Otherwise:
- if the value before ? is true then replace this ternary expression as the value of the ternary expression between ? and :
- if the value before ? is false then replace this ternary expression as the value of the ternary expression after :
Hint: You can apply the idea of a syntax tree to solve this problem.
Input
The first line of the input is a valid ternary expression that contains the ternary operators and value indices.
- It is guaranteed that the value indices are pairwise distinct and range from 1 to the number of values in this ternary expression.
- For example, in the sample input below, the number of values is 5, and the value indices from left to right is 5, 3, 2, 4, 1, respectively.
The next line contains a single integer T, (T <= 5000), representing the number of combinations you have to evaluate.
For the next T lines, each line contains a binary string whose length is equal to the number of values in the ternary expression, giving the setting of each value.
- Note that the i-th character in this binary string (counted from left) is for the value index i. (1 represents true and 0 represents false)
- For string "01101", value indices 1-5 are set as 0,1,1,0,1, respectively.
There are 5 testcases in this problem.
For the first 3 testcases: 1 <= number of values <= 5
For the rest of the testcases: 1 <= number of values <= 3001
Output
For each combination, output the value of the ternary expression. (1 represents true and 0 represents false)
Remember to add a newline character at the end of every line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given several prefix expressions, each representing a function. Such an expression has at most 4 types of operations and 5 variables, described below.
We explain the 4 types of operations using infix:
- Addition. ‘a+b’ means a plus b, in which a, b are integers.
- Subtraction. ‘a-b’ means a minus b, in which a, b are integers.
- Multiplication. ‘a*b’ means a times b, in which a, b are integers.
- Function call. ‘f@a’ means return the value f(a), in which f is a function and a is an integer.
For variables, they are all integers, and the 5 variables are A, B, C, D, and X, respectively. For A, B, C, and D, you will get their values from input. For X, it is the parameter that you gave the function.
The function name will be a lowercase letter. Given the function name and the prefix expression of each function. Now here are q queries: given the function name and the parameter (i.e., X) for the function, and the values of A, B, C, and D, please output the calculation result.
For sample input 2, here are the syntax trees for the 2 functions.
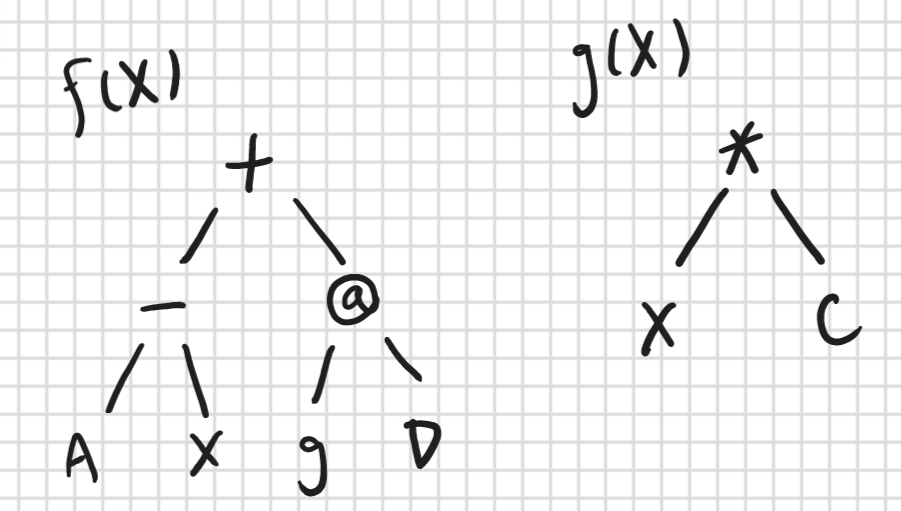
Note the parameter X for the functions are different. For example, in the second query, it’s 1 for f and it’s 5 for g.
Input
The first line contains two integers, n and q, which means there are n functions and q queries.
Each of the following n lines contains a lowercase letter representing the function name, and a string representing the prefix expression, separated by a space.
Each of the last q lines contains a lowercase letter and five integers, separated by spaces, representing the function name, the parameters X, A, B, C, and D, respectively.
Constraints:
1 ≤ n ≤ 26
1 ≤ q ≤ 100
-1000 ≤ A, B, C, D, X ≤ 1000
The expression would not contain over 200 characters.
For cases 1~3, the expressions only contain the first 3 operations.
For other cases, no further constraints.
Output
An integer that represents the calculation result. Since the answer could be large, please output the answer modulo 998244353. After modulo, the answer should be between 0 ~ 998244352.
Note
Since the answer should modulo 998244353, you should take the remainder after every operation (including returning the value of a single variable). Since the result of taking the remainder must be non-negative, the result should add 998244353 if it is negative after modulo. Be free to use the following function:
num %= 998244353;
if(num < 0) num += 998244353;
return num;
}
Sample Input Download
Sample Output Download
Tags
Discuss
Description
What is a Perfect Binary Tree?
A perfect binary tree is a binary tree data structure with the following characteristics:
- Every level of the tree is completely filled with nodes. In other words, each level has the maximum number of nodes possible for that level.
- Each node in the tree has either two children or no children, and a node that has no children makes it a leaf node.
- The total number of nodes in a perfect binary tree of height h is 2h+1 - 1. (Note that the height of the following example tree is 2 not 3.)
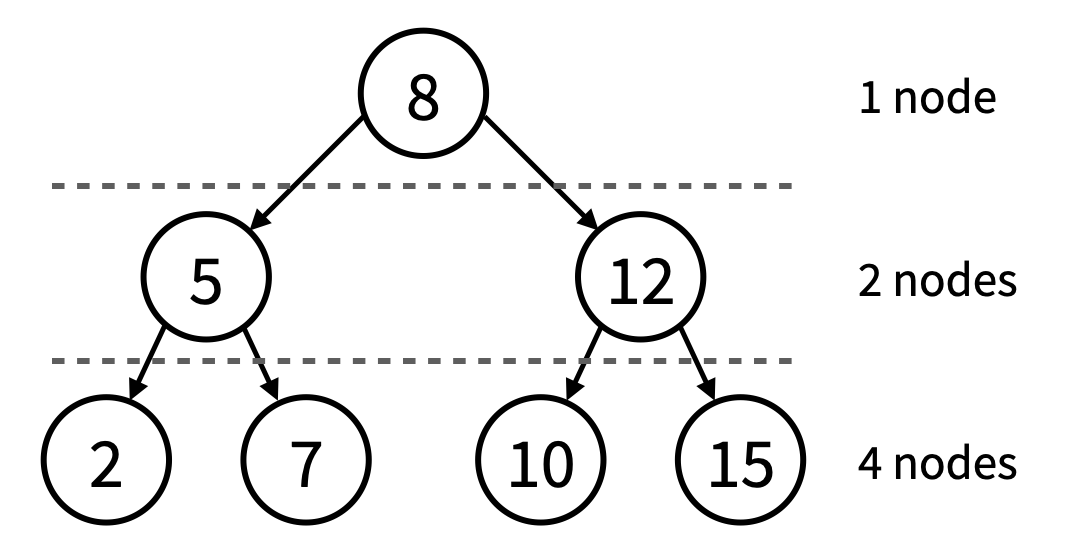
What is a Binary Search Tree?
A binary search tree (BST) is a binary tree data structure with the following properties:
- Each node in the tree has at most two child nodes (binary tree).
- For any node, its value is greater than or equal to the values stored in the left subtree.
- For any node, its value is smaller than the values stored in the right subtree.
- For any node, the left subtree and the right subtree are binary search trees respectively as well.
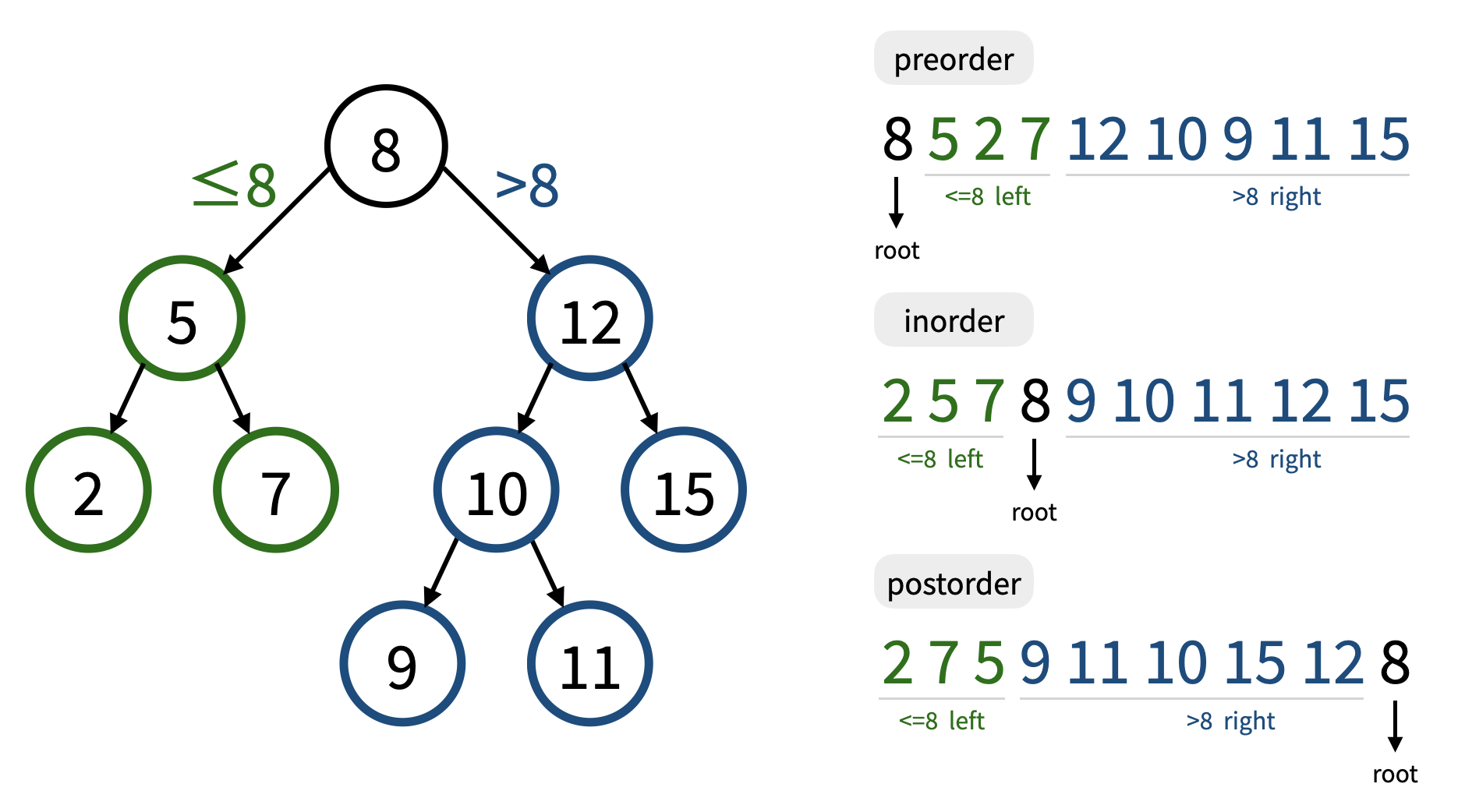
We know that the preorder traversal is based on the order "root -> left subtree -> right subtree". Therefore, for the preorder traversal sequence of a binary search tree, we can observe that the first number is the root of the tree, and in the following sequence, numbers smaller than or equal to the root belong to the left subtree (green part), while numbers larger than the root belong to the right subtree (blue part).
In this problem:
You are given the preorder sequence of a scrambled perfect binary search tree with unique node values, where the left and right subtrees of several nodes of the original tree have been swapped. See the following example of swapping node 8's and then node 12's left and right subtrees.
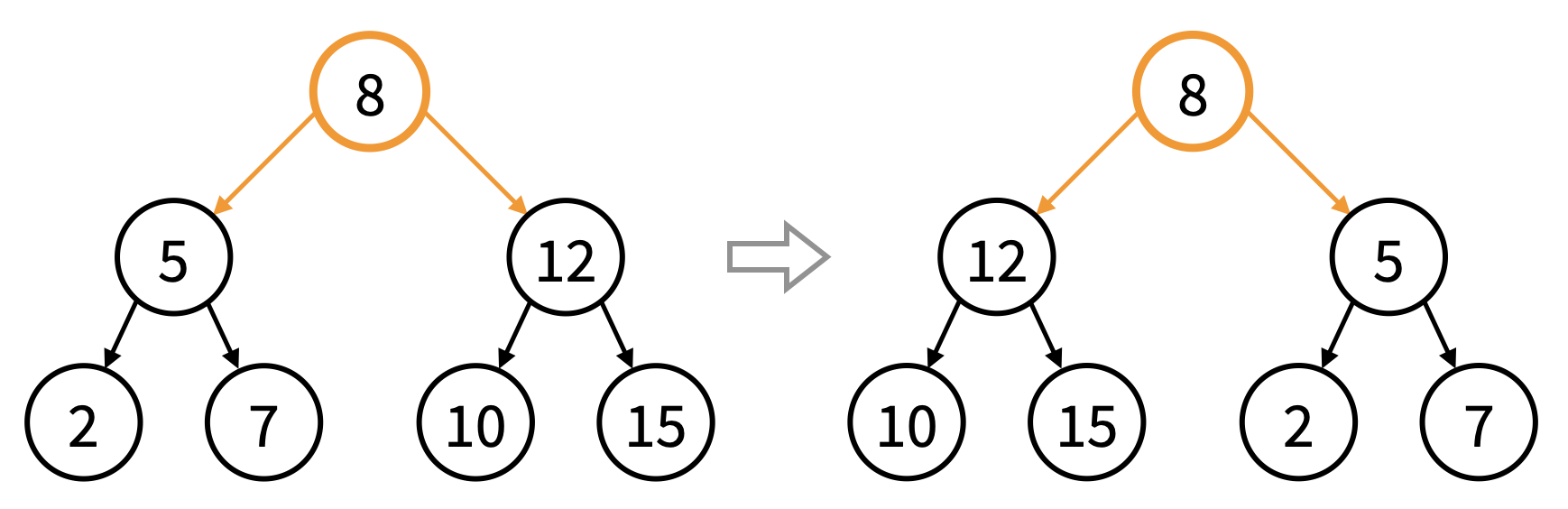
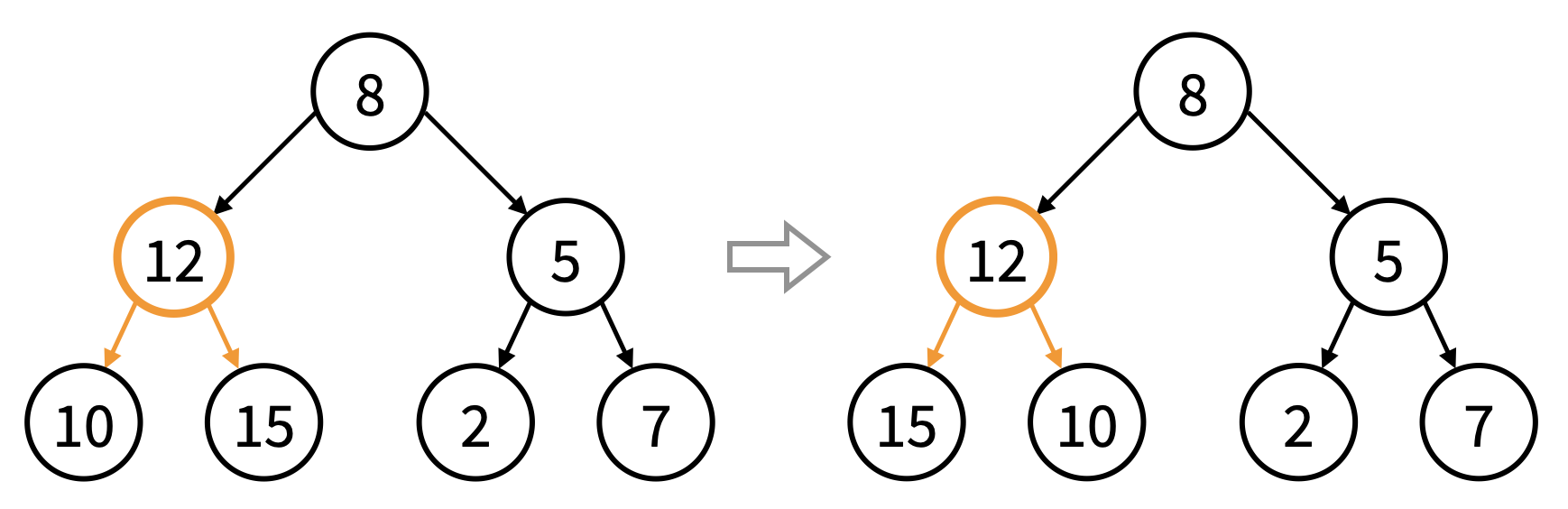
Can you help us reconstruct the original binary search tree and output its postorder sequence?
Input
- The first line contains an integer N (1 ≤ N ≤ 105) - the length of the preorder sequence for the scrambled perfect binary search tree.
- The second line contains N integers x1, x2, ..., xN (1 ≤ xi ≤ 109) - representing the preorder sequence.
Output
Output one line that contains N integers - representing the postorder sequence of the original perfect binary search tree. Remember to print '\n' at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Today when you stepped out of your house, you saw something fall from the sky and land at the park near your house. You felt worried and curious, so you ran quickly toward the park to check it out. Fortunately, the falling thing isn’t a plane, a bomb, or something harmful, and it is just a binary tree breaking into pieces. Additionally, there was a paper by its side. You picked up the paper and realized that it is the information of the binary tree. Since the binary tree's live matters, you collect the breaking pieces of the binary tree to your house and decide to reconstruct it.
So here’s the problem.
You will get some information about a binary tree:
- The inorder sequence.
- (n-1)/2 pairs of nodes, in which the nodes in the same pair have the same parent.
Please print the preorder of the reconstructed binary tree.
It is guaranteed that the tree exists and is unique, and each node would either have no child or 2 children. Note that there's no fixed order for the pairs, and the first node of a pair is not necessarily the left child.
Hint:
- You can use the following algorithm.
- Let the root node be the one that does not appear in any child pair.
- Starting from the root, find the child pair in which one node is to the left and one node is to the right of the root in the inorder sequence, and repeat the process recursively.
- Consider the following example.
Input
The first line contains an integer n, which means there are n nodes in the binary tree.
The second line contains n integers, representing the inorder sequence.
Each of the following (n - 1)/2 lines contains two integers, which means the two nodes have the same parent.
Constraints:
n % 2 == 1
Cases 1~7: n < 10
Cases 8~11: n < 3000
The inorder sequence contains n distinct numbers. For each number x, 1 ≤ x ≤ n.
Output
A line that represents the preorder sequence.
Please print ‘\n’ at the end.