| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11110 | cheat_sheet (mid2) |
|
| 11711 | Dynamic 3D array |
|
| 13724 | Doraemon plays Tetris with gadgets |
|
| 13733 | Cookie Monster: Let's Reverse |
|
Description
printf() and scanf() format
printf("%d", n);
FORMAT ARGUMENT TYPE
%d, %i int decimal
%u unsigned int
%x unsigned int hexadecimal
%#x unsigned int hexadecimal with prefix 0x
%f double
%Lf long double
%e, %E double scientific notation
%c int to print a character
%s char * string (character array ended with '\0')
%p void * print memory address
%g, %G double %f or %e depending on the length
scanf("%d", &n);
FORMAT ARGUMENT TYPE
%d int * &n, store the input integer in n
%ld long *
%lld long long *
%u unsigned int *
%f float * read float
%lf double * read double
%Lf long double * read long double
%c char * read 3 characters %3c
%s char * read a string until whitespace
%n int * with %s, to get string length
char a[100]; int len;
scanf("%s%n", a, &len);
len will have the string length
Frequently used functions
#include <string.h>
char str[10];
scanf("%s", str);
to get the string length using strlen(str)
to compare two strings strcmp(str1, str2) ==0 if equal
to compare the first n chars of two strings strncmp(str1, str2, n) ==0 if equal
to copy str2 to str1 strcpy(str1, str2)
to append a copy of str2 to str1 strcat(str1, str2)
to copy the first n chars of str2 to str1 strncpy(str1,str2, n) remember to add '\0' to str1
#include <ctype.h>
isspace(ch), islower(ch), isupper(ch), isdigit(ch)
isalpha(ch), toupper(ch), tolower(ch)
To create a 5-by-5 two-dimensional array, we need to write
int a[5][5];
It will be indexed as follows:
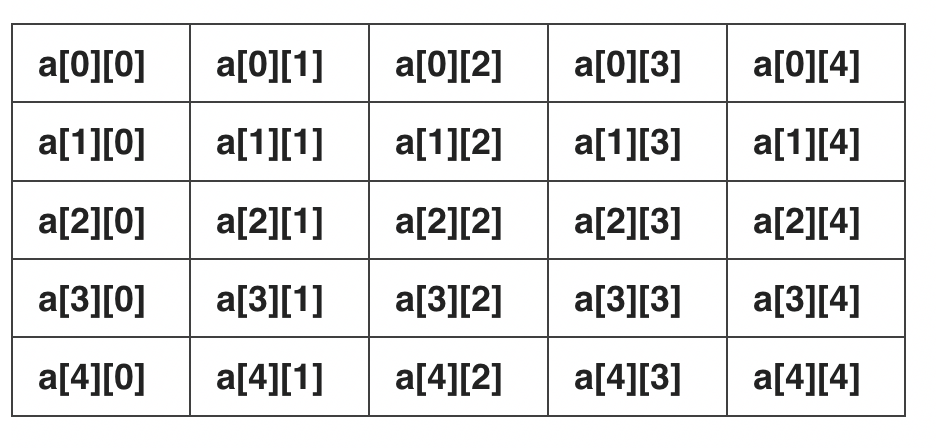
How to read the following data?
1 2 3 4 5 e
#include <stdio.h>
int main(void)
{
int x;
while (scanf("%d", &x) == 1) {
printf("x=%d\n", x);
}
return 0;
}
How to read the following data?
2
L 5 2
D 5 3
#include <stdio.h>
int main(void)
{
char ch;
int i, n, row, col;
scanf("%d", &n);
for (i=0; i<n; i++) {
while(getchar()!='\n');
scanf("%c%d%d", &ch, &row, &col);
}
return 0;
}
Using for loops to print a two-dimensional array
for(i = 0; i < row; i++) {
for (j = 0; j < col; j++) {
printf("%5d", A[i][j]);
}
printf("\n");
}
Using bubble sort to rearrange an array ap
for (i = 0; i < n-1; i++)
{
for (j = 0; j < n-1-i; j++)
{
if (ap[j] > ap[j + 1])
{
temp = ap[j];
ap[j] = ap[j + 1];
ap[j + 1] = temp;
}
}
}
operators:
! && || == != + - * / %
> < >= <=
How to avoid common errors and how to debug for OJ
1. Put the arrays in the 'global' area. Set their size bigger than required. Avoid using variable-length arrays (e.g. int arr[n];). Keep the array size fix (e.g., int arr[1000];).
2. After writing the code for reading input data, you may print out the data to check if your code reads them correctly. Do not proceed to write subsequent code before you confirm that.
3. If your program crashes, usually it is caused by memory related errors. Check the ranges of for-loops to see if your code attempts to read or write the elements out of the arrays’ boundary.
*(a+i) is equivalent to a[i]
(a+i) is equivalent to &a[i]
Input
Output
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In this problem, you are asked to design two functions
1.
unsigned*** new_3d_array(unsigned n,unsigned m,unsigned k);
malloc an n*m*k 3D unsigned array, and then return its address. The main function will check the correctness of your array.
2.
void delete_3d_array(unsigned ***arr);
Free the memory space of your array that was previously allocated by using malloc. Be careful about the memory uage of your program allocated dynamically so as to avoid MLE.
The two functions have been declared in function.h, and you are asked to complete the function definitions in function.c.
Your program should construct the 3D array by using only three malloc function calls. Notice that malloc is a time-consuming operation.
Note: for OJ submission:
Step 1. Submit only your function.c into the submission block. (Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
Please refer to the main function.
The input only has one line, consisting of five positive integers t,n,m,k,r separated by space characters, where t is the number of tests, (n,m,k) represents the array size, and r is a parameter for testing.
Note that n*m*k<=10000000 and t*n*m*k<=60000000
Output
In order to test your array's correctness, we will use your array to do some computations and output the results.
Sample Input Download
Sample Output Download
Partial Judge Code
11711.cPartial Judge Header
11711.hTags
Discuss
Description
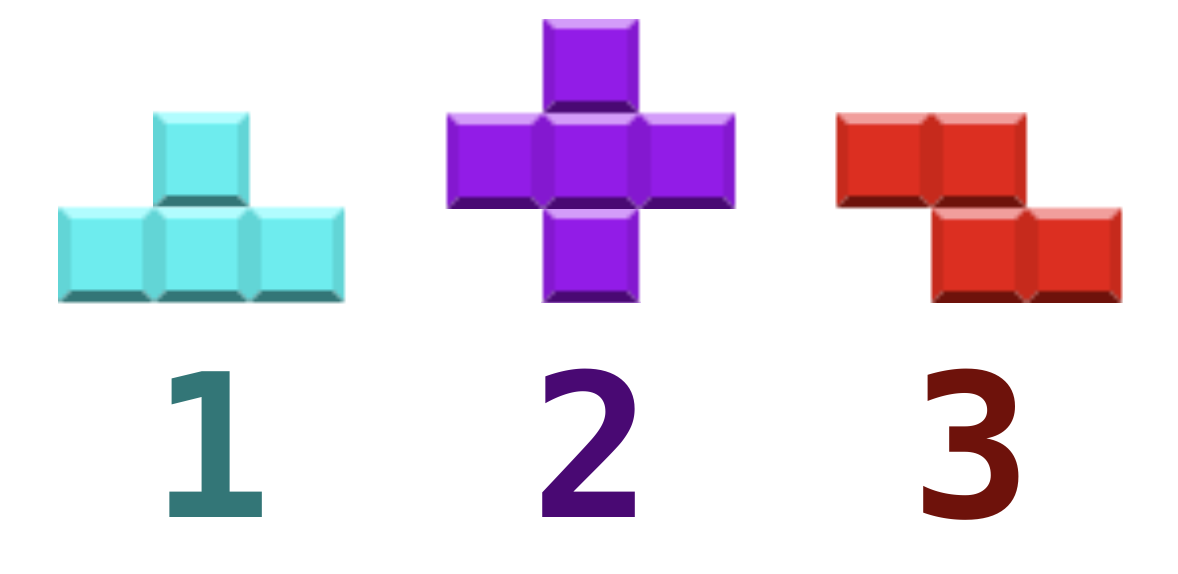
Besides the shapes of tetrominoes and the width of the playing field, the basic description of this problem is the same as that of "13722 - Doraemon plays Tetris". (See the highlight of this part in red color.)

Doraemon's favorite video game is Tetris (俄羅斯方塊).
In Tetris, players complete lines by moving differently shaped pieces (tetrominoes), which descend onto the playing field. The completed lines disappear and grant the player points, and the player can proceed to fill the vacated spaces. The game ends when the uncleared lines reach the top of the playing field. - Wikipedia
You may refer to the gif for more detail demonstrating this game.
In this problem, we want to simulate the gaming process of Tetris, and several rules differ from the original Tetris:
- The playing field width is 4, and we have only 3 types of tetromino shapes.
- When the tetrominoes form a horizontal line, the line won't be disappeared but remains in the same place.
- You can only rotate the tetrominoes before you drop them into the field; you must decide the directions of the tetrominoes first and choose the place you want to put them in. The tetromino would fall until it touches the ground or the other tetrominoes.
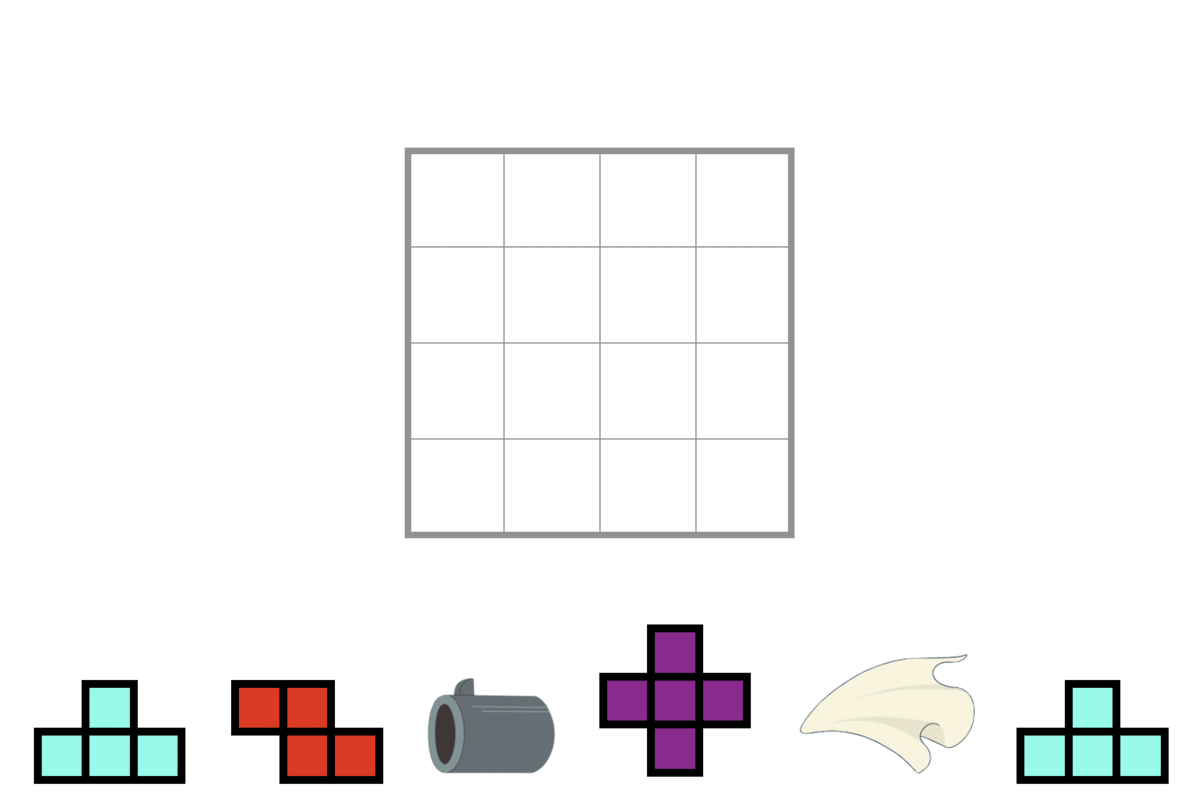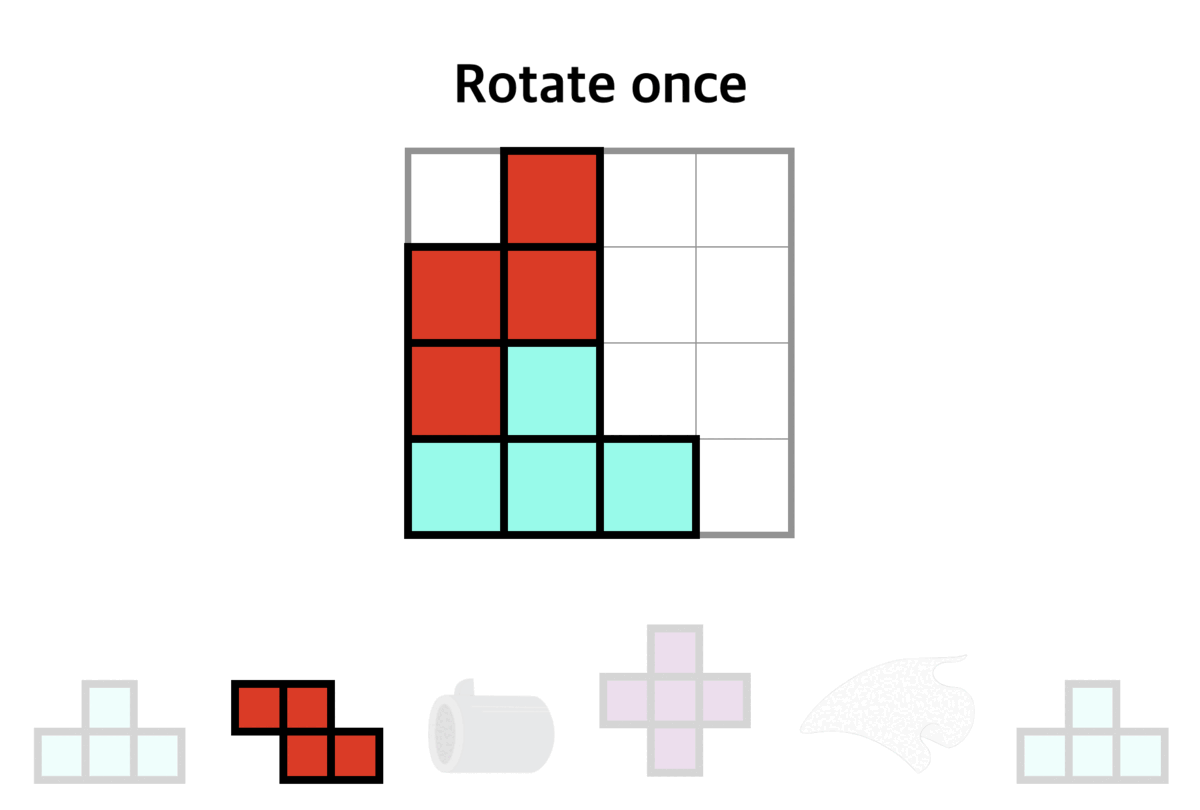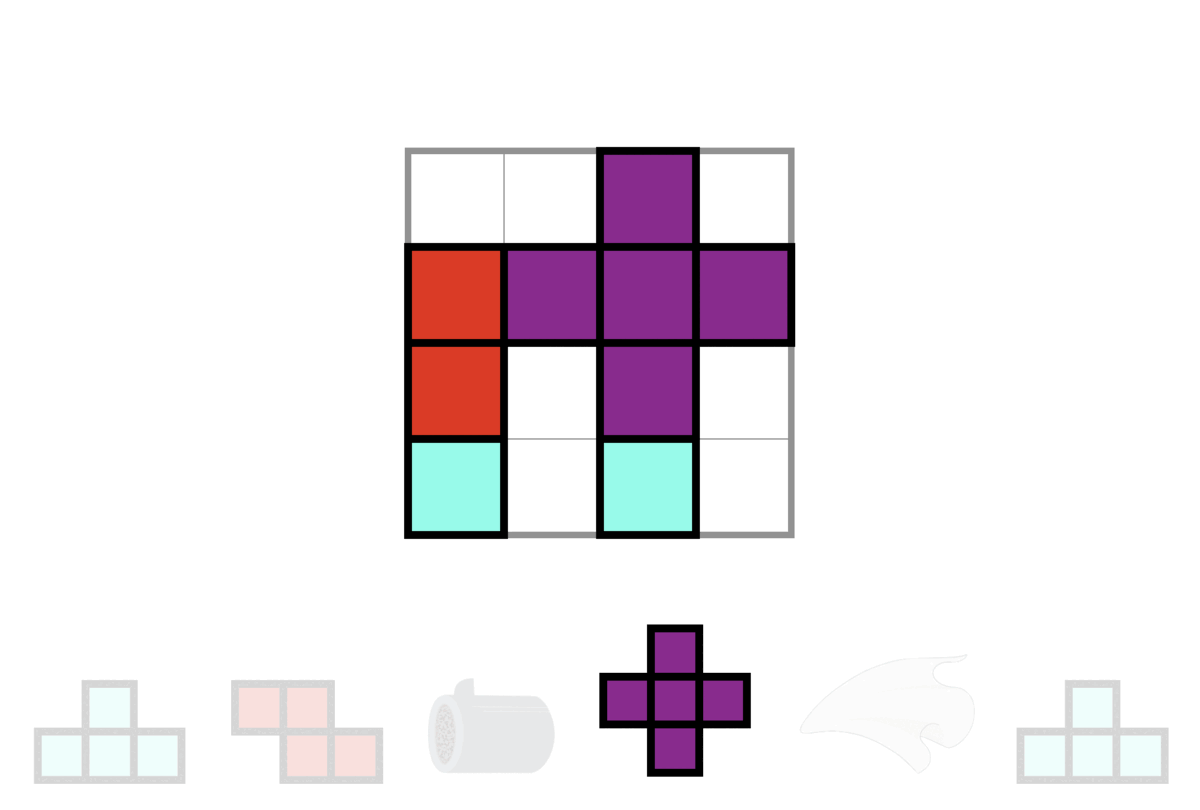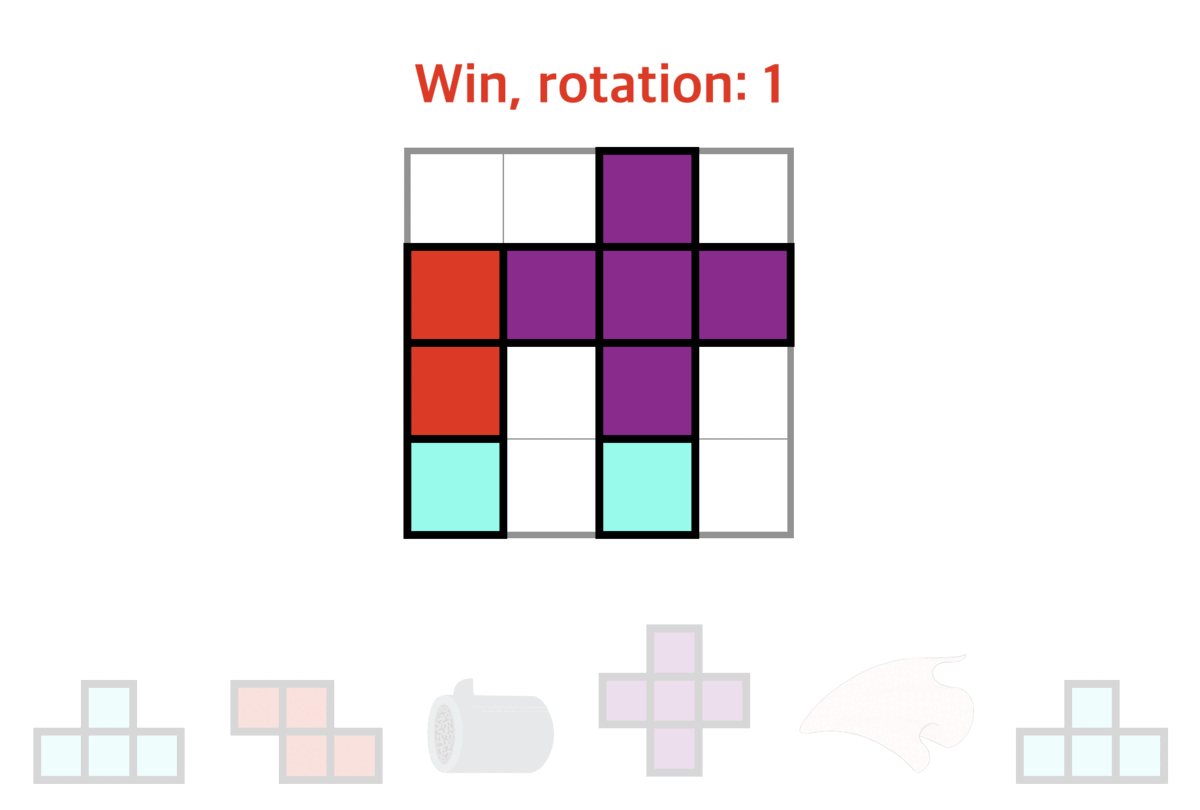
The following figure shows the 3 types of tetrominoes. Please notice that their shape differs from "13722 - Doraemon plays Tetris".
Given a sequence of the tetromino type, you must put it into the playing field by order.
If we put a tetromino into the field that the height of the stacked tetromino would exceed the top of the playing field, then the game would fail. In this problem, you only need to determine whether the game will end successfully; we can put all the tetrominoes into the field, and no tetromino exceeds the top of the playing field. (Notice: exactly reaching the top is acceptable in this problem)
If the game failed in the end, tell the game would end at x-th tetromino. Since we want to maximize the possible game time, please output the largest x.
******In this problem, please also notice the following part.
Since Doraemon keeps losing this game, he decides to use his gadgets (道具) to cheat on this! Symbols of two types of gadgets would appear in the sequence of the tetrominoes, representing the moment he can use them. You don't need to use them if you believe better strategies exist. If you choose to use a given gadget, you can only use it at the moment it occurs in the sequence, and the gadget can not be stored and used in the future.
Type 1: Air Cannon

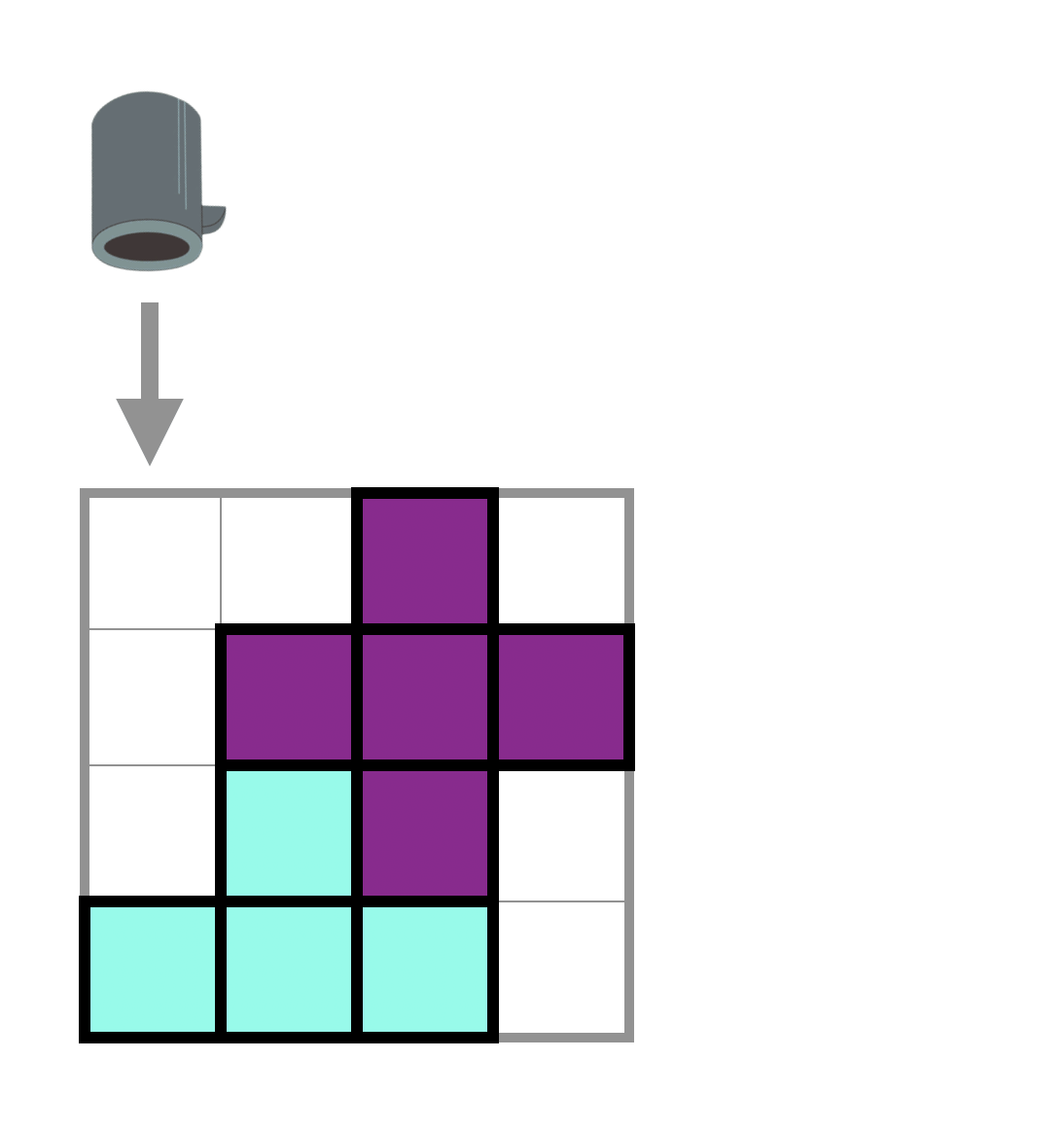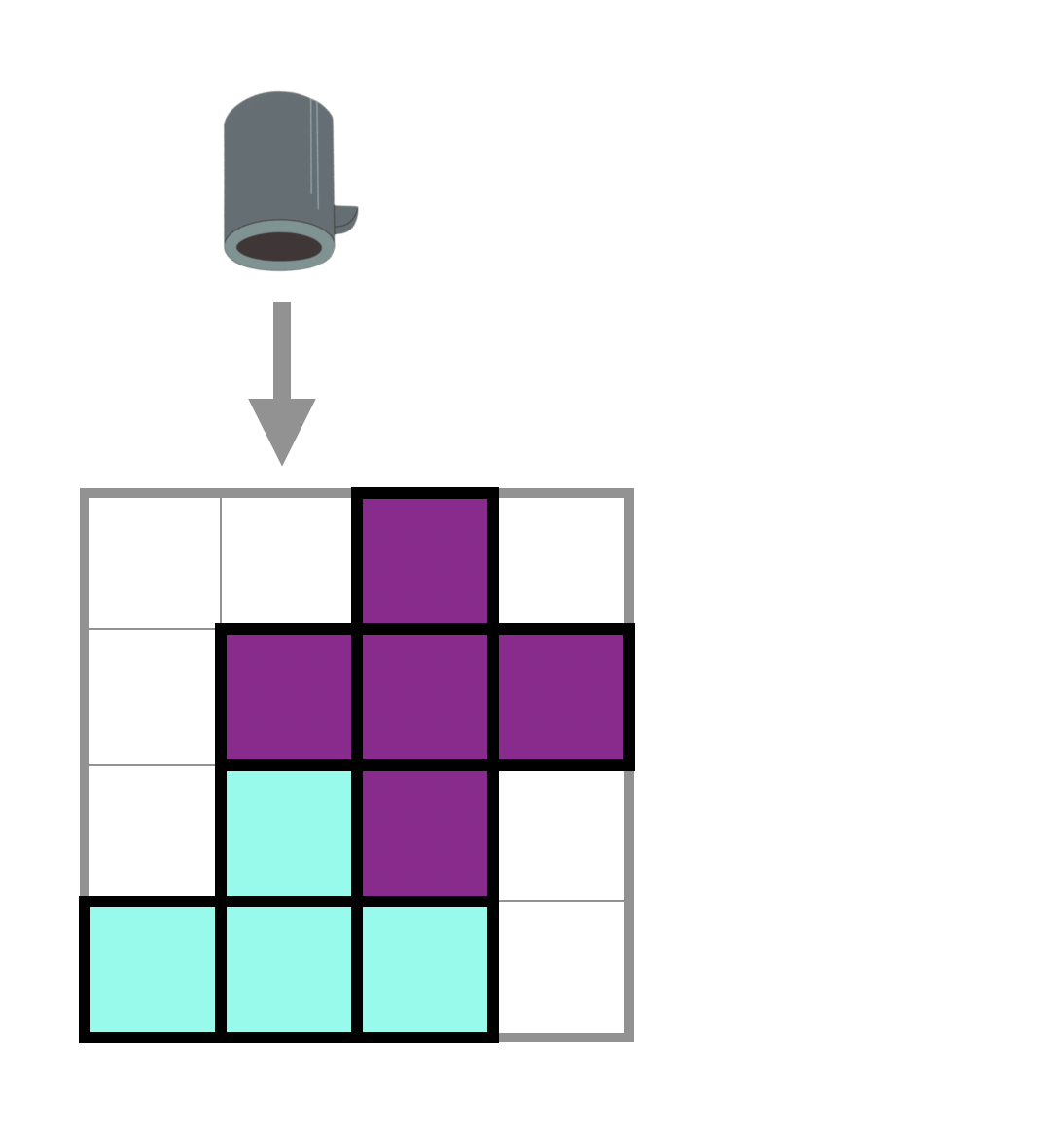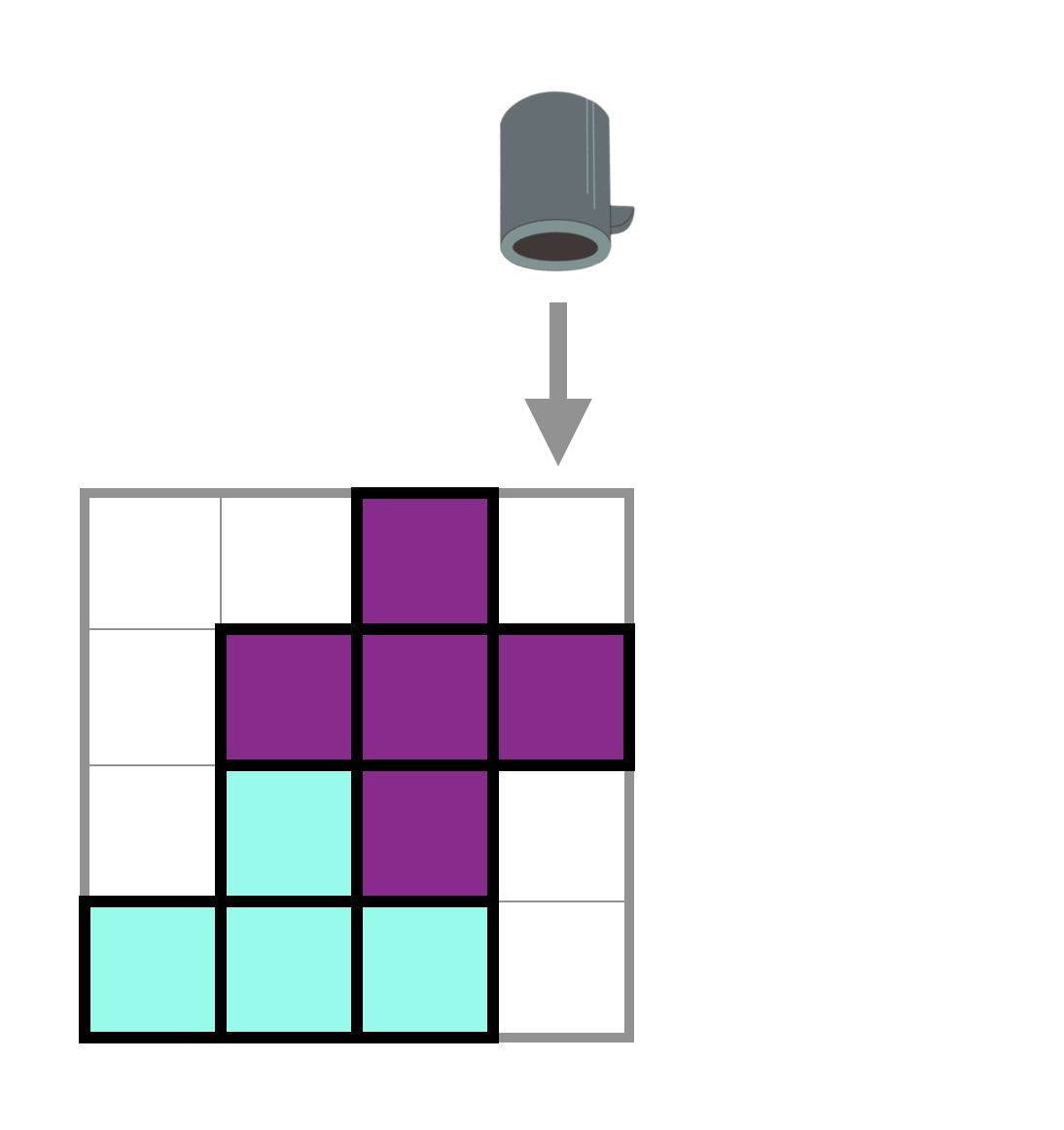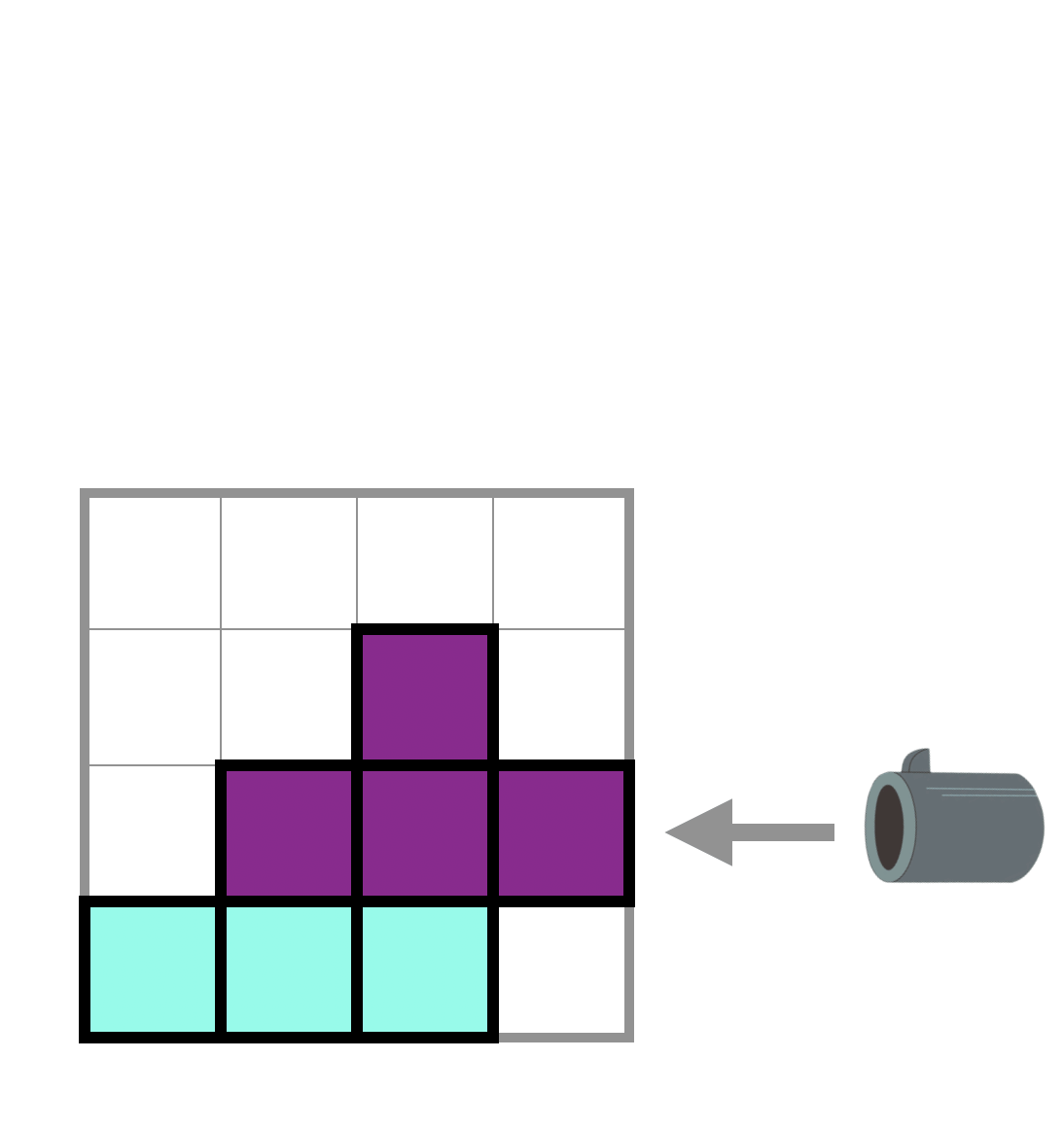
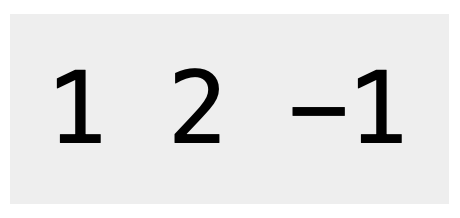
Using this type of gadgets, you can remove a specific row or column of the playing field. If you choose to remove a row of the playing field, all the remaining pieces above will descend by one block. We use -1 to represent this type of gadgets in the given sequence.
Type 2: Invisible Cape

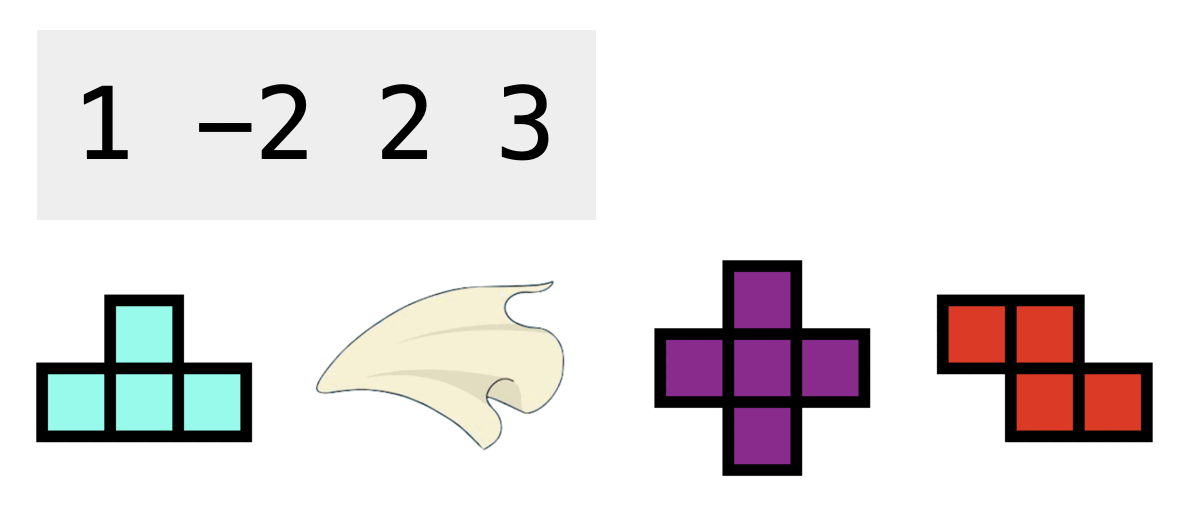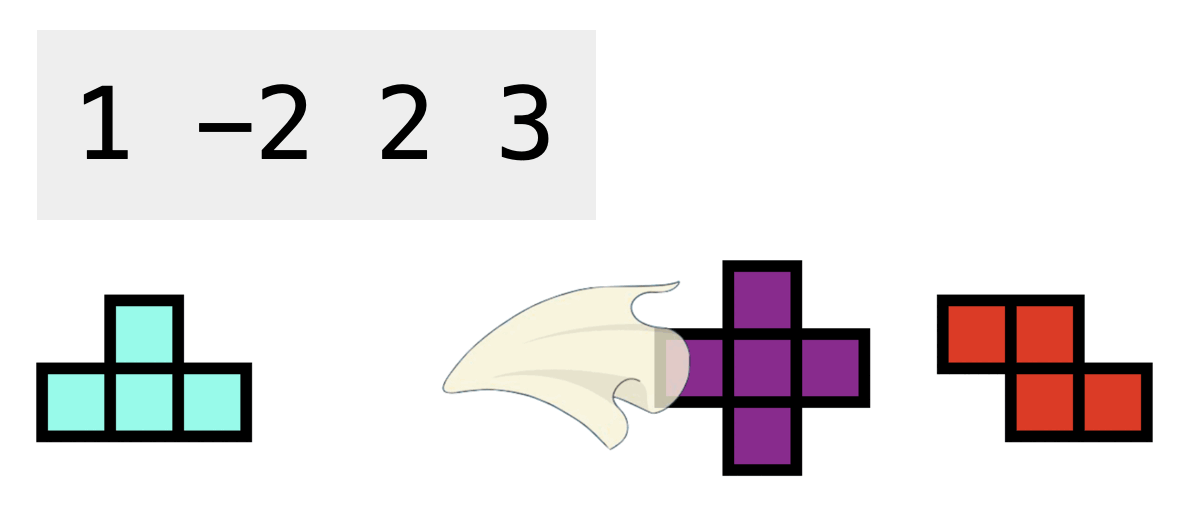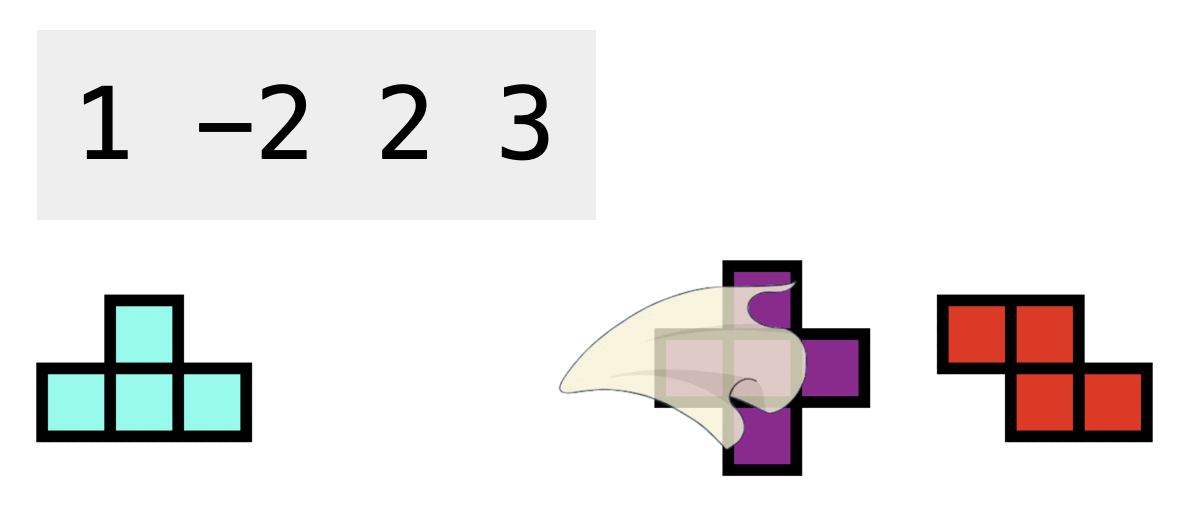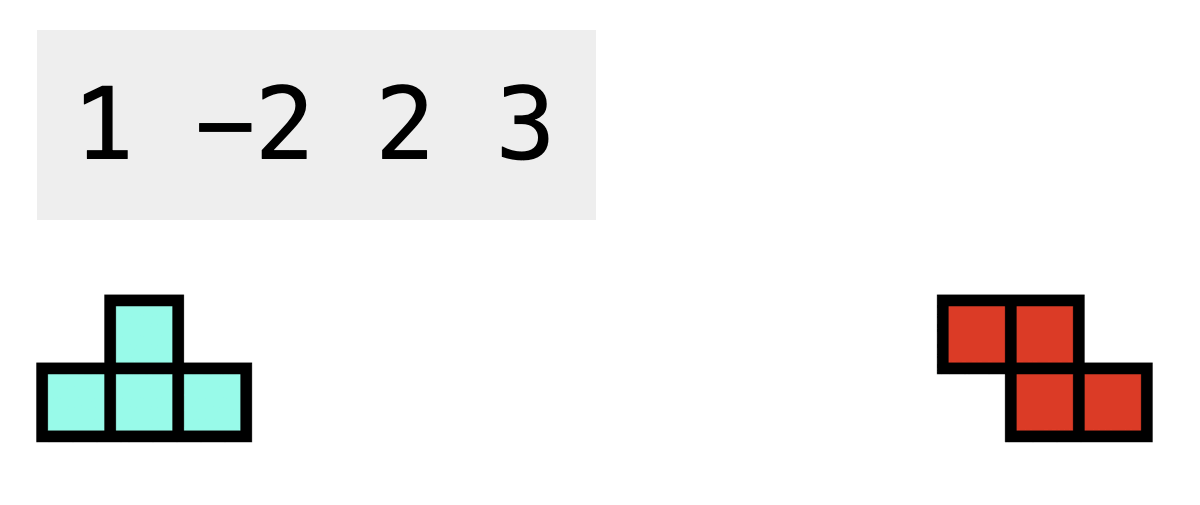
Using this type of gadgets, you can ignore the next upcoming tetromino, and we guarantee that it always comes before a tetromino in the sequence. This type of gadgets can only apply to the tetromino immediately after it. We use -2 to represent this type of gadgets in the given sequence.
You may refer to the following test case 2 demonstration to learn more about the operation of the gadgets.
Since Doraemon is extremely lazy, he wants to minimize the number of "clockwise rotations" of tetrominoes. If he can win the game, please tell him the minimum times of clockwise rotations that are required.
So, in this problem:
- If Doraemon can win this game, calculate the minimum number of clockwise rotations.
- Otherwise, calculate the largest x that Doraemon would lose at the x-th term of the sequence. We can observe that the x-th term of the sequence must be a tetromino.
Test case constraints
Since Doraemon still needs to improve at this...
- 1~5: We guarantee that there won't have any gadgets in the sequence, and Doraemon will always lose
- 6~8: We guarantee that if Doraemon can win, the minimum number of times for the rotation must be 0
- 9~10: No further constraints in these test cases
Input
The first line contains a positive integer T ≦ 10, representing the number of test cases.
For each test case:
The first line contains two positive integers N, H ≦ 20, representing the tetrominoes' sequence length and the playing field's height. The second line contains N integers, which can be 1, 2, 3, -1 or -2, representing the type of each tetromino or gadget.
Output
For each test case, output one line.
- If Doraemon can win the game with a minimum of x times of clockwise rotations, print "Win, rotation: x\n".
- Otherwise, the game would end at the x-th term of the sequence, and you should print "Lose at x\n".
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Today, as usual, the cookie monster is picking the cookies to eat for this meal. He is so tired and unable to select the cookies he wants since he was busy preparing for his midterm and didn’t sleep last night. As his good friend, you decided to help him so he doesn’t need to worry about his lunch.
There are n cookies in the shop. For each cookie, there is a number di, representing how yummy the ith cookie is. In general, the larger di is, the more delicious the ith cookie is. However, due to some unknown reasons, the cookie monster especially loves cookies that contain the digit 7 in their di. For example, the digit ‘7’ appears twice in 7927 and appears once in 70. If there are more digits ‘7’ appearing in di for a cookie, the cookie monster would tend to choose that cookie first.
Moreover, here’s your cookie-choosing strategy:
- For any two cookies, always choose the one that with more ‘7’ appears in di first.
- If there are two cookies containing the same amount of ‘7’ in their di, choose the one with larger di.
However, due to some unknown reason, the number di does not always be marked on the wrapper of the cookie directly. Let si denote the string printed on the wrapper of the ith cookie. si is a string containing only integers and dots. There may be no dots or exactly 2 dots in si. If there are 2 dots in si, reversing the interval between 2 dots and then removing the dots can transform si into di. For example, if si = 31.124.12, then di = 3142112. If si doesn’t contain any dots, then di = si.
Now the cookie monster wants to choose k cookies at most for this meal, help him choose the cookies he is going to eat.
For testcase 1 and 2, there are no dots in si for every cookie.
For testcase 3 and 4, if there are 2 dots in si, it is guaranteed that the substring between 2 dots is a palindrome, i.e. the substring remains the same after the reversal.
There are no further restrictions for the remaining testcases.
Input
The first line contains two integers n, k, representing the number of cookies in the shop and the amount cookies you are going to choose, respectively.
The next n lines each contains a string, The 1+ith line specifies the value of si.
Constraints:
1 ≤ n ≤ 1000
1 ≤ di ≤ 10300
1 ≤ k ≤ n
1 ≤ |si| ≤ 300
It is guaranteed that there are no leading zeros in si and after transforming si to di.
Output
Output k lines, the value of di for each cookie you choose, in the order that the cookie monster likes more prints first.