| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11711 | Dynamic 3D array |
|
| 11712 | Morse code |
|
| 12510 | Hakka's Maze |
|
| 12515 | Little Brick's Dream |
|
| 13722 | Doraemon plays Tetris |
|
| 13723 | Cookie Monster |
|
Description
In this problem, you are asked to design two functions
1.
unsigned*** new_3d_array(unsigned n,unsigned m,unsigned k);
malloc an n*m*k 3D unsigned array, and then return its address. The main function will check the correctness of your array.
2.
void delete_3d_array(unsigned ***arr);
Free the memory space of your array that was previously allocated by using malloc. Be careful about the memory uage of your program allocated dynamically so as to avoid MLE.
The two functions have been declared in function.h, and you are asked to complete the function definitions in function.c.
Your program should construct the 3D array by using only three malloc function calls. Notice that malloc is a time-consuming operation.
Note: for OJ submission:
Step 1. Submit only your function.c into the submission block. (Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
Please refer to the main function.
The input only has one line, consisting of five positive integers t,n,m,k,r separated by space characters, where t is the number of tests, (n,m,k) represents the array size, and r is a parameter for testing.
Note that n*m*k<=10000000 and t*n*m*k<=60000000
Output
In order to test your array's correctness, we will use your array to do some computations and output the results.
Sample Input Download
Sample Output Download
Partial Judge Code
11711.cPartial Judge Header
11711.hTags
Discuss
Description
Morse code is a way to represent English letters (here we only consider capital letters). The code is composed of some long signals and some short signals. For convenience, we represent a long signal as '-' and represent a short signal as '*'. Then ‘/’ is used to serve as a blank that distinguishes each word that consists of several letters.
For example, ''NPSC GG'' is ''-* *--* *** -*-* / --* --*", where “-*” = N and “*--*” = P, and the code for other letters is shown below.

However, these long and short signals in the Morse code cannot be represented using gesture. A way to simulate the long and short signals is as follows:
- “===” represents a long signal. (hitting table for 3 times)
- “=” represents a short signal. (hitting table for 1 time)
- For a letter, “.” is used as a pause to separate signals.
- In a word, “…” is used as a pause to separate letters.
- “…….” is used to separate words (that is, to represent ‘/’ as mentioned above).
For example, “NPSC GG" can be encoded as follows:
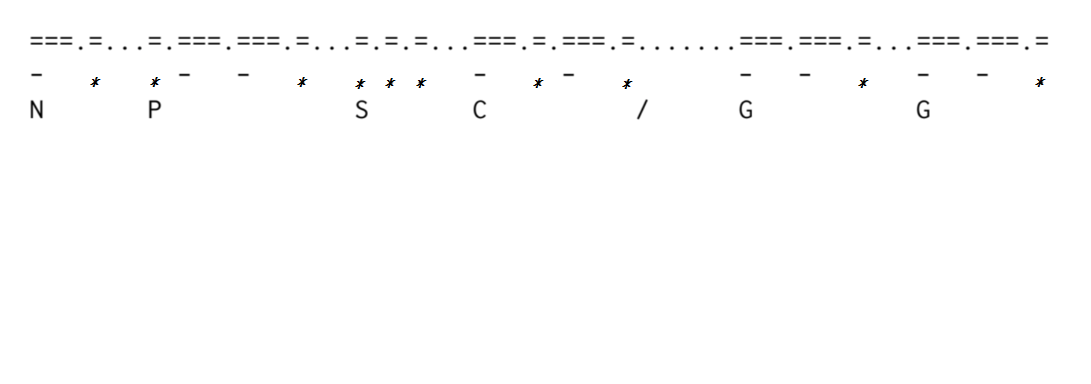
P.S the problem is from 2015 網際網路程式設計全國大賽
Input
There are two lines. The first line is an integer N, meaning the second line will give a string with length N, and this string is only composed of '=' and '.'.
.N <= 999.
.The output string begins and ends with a non-blank letter.
Output
Print the result after decoding
Following is a sample test case:
Input:
57
=.===...===.=.=.=...===.=.===.=...===.=.=...=...=.=.===.=
Output:
ABCDEF
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In the village of hakka's, there are lots of big big mazes,
it is said that the delicious hakka mochi(麻糬) is hidden in one of the secret maze.
You, a poor programmer, work for hakkas without getting any paid,
want to find out the secret, and change the job to selling mochi,
since being a programmer is too tired, and may be died overworked.
So, one day, you sneaked into the village head's house, and stolen all the mazes' maps out.
You have got T maps,
and each map shows that the maze is N*M grids big,
and start from (1,1) (the left top corner), and the mochi is at (N,M) (the right bottom corner),
the '#' on the map represent the wall,
and the '*' on the map represent that you can walk pass that grid,
and the 'T' on the map represent the teleport device.
Walking in the hakka's maze, start from the starting point,
if you are standing on a road,
you can go to the up, right, left, or the bottom grid near you,
you cannot be on the wall,
and if you are standing on a teleport device,
you can go to the up, right, left, or the bottom grid near you, too,
but you can also teleport to any other teleport device.
You want to make sure the if it is possible to walk from the starting point (1, 1) to the ending point (N, M) of each map,
so you won't waste time finding the mochi.
ouo.
For Example, if the input is:
1
3 3
***
*#*
##*
The output should be 'Yes' (without quotes),
since you can go (right, right, down, down) to get to the ending point of the map.
Input
The first line of the input is a number T,
represent the amount of map you have.
Start from the second line, there are T maps,
the first line contains 2 number N, M, represent the maze is N*M big,
then the following N lines are M characters,
the character '#' represent the grid is a wall,
the character '*' represent the grid is a road,
the character 'T' represent the grid is a teleport device.
It is guarantee that,
for all test cases, T <= 10, 2 <= N, M <= 1000,
for the 1 test case, 2 <= N, M <= 10,
for the 2, 3 test cases, 2 <= N, M <= 200
for the 3, 6 test case, there are no teleport device.
for the 4, 5, 6 test cases, 2 <= N, M <= 1000
and (1, 1) will not be a wall.
Output
Output T lines,
if it is possible to walk from the starting point to the end point,
output 'Yes', otherwise, output 'No'. (Without quotes)
Sample Input Download
Sample Output Download
Tags
Discuss
Description
As you know, Little Brick is a student is NTHU, major in CS,
he often told his friends that he have a dream - Grow Taller.
He said that every time he lines up in a queue,
he cannot see anything since there are always someone taller than him,
and standing in front of him.
He is furious, he hate to stand after people who is taller than him,
so, he define a formula to calculate the confort level of standing in the ith position in a line.
The confort level f(i) is defined as the number of consecutive people standing in front of him, and are shorter than him.
That see if there is a line, and their heights are 150, 170, 180, 160, 165, fron front to end,
then f(1)=0 since there are no anyone standing in front of position 0,
f(2)=1, since 150 < 170,
f(3)=2, since 170 < 180 and 150 < 180,
f(4)=0, and f(5)=1
One day, Little Brick told you that he is waiting in a long line,
looking forward to shaking hand with his favorite idol,
which is your favorite one, too.
You called Little Brick and asked: "Where are you, Little Brick",
and Little Brick replied: "I am at the position where the comfort level is X",
you: "Wait, what the f...", but it was too late, he had already hang up the phone.
Now, inorder to find Little Brick so that you can cut in line to shake hand with your favorite idol,
you need to find where Little Brick may be at.
That is, given you 2 integers N and X,
where N is the number of people in the line,
and X is the comfort level Little Brick at.
Then N distinct numbers Ai,
representing the height of the people standing at the ith position,
from the front to the end,
you need to find all possible position where Little Brick may be at.
ouo.
For example, the sample input:
6 2
3 1 6 2 4 5,
we can calculate the formula of all index,
f(1)=0, f(2)=0, f(3)=2, f(4)=0, f(5)=1, f(6)=2,
and X=2, so Little Brick may be at position 3 or 6.
Input
The first line contains 2 integer N, X,
N is the number of people, and X is the comfort level,
the second line contains N integer Ai, separate by a space,
representing the height of people standint at the ith position.
It is guarantee that,
1<=N,X<=10^7,
1<=Ai<=10^9
Output
Output contains one line,
output all possible positions where Little Brick may be at,
separate by a blank.
If there is no possible position where Little Brick may be at,
output a single line "ouo" (without quote).
The index of position start from 1, and you must output the index in increasing order.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Doraemon's favorite video game is Tetris (俄羅斯方塊).
In Tetris, players complete lines by moving differently shaped pieces (tetrominoes), which descend onto the playing field. The completed lines disappear and grant the player points, and the player can proceed to fill the vacated spaces. The game ends when the uncleared lines reach the top of the playing field. - Wikipedia
You may refer to the gif for more detail demonstrating this game.
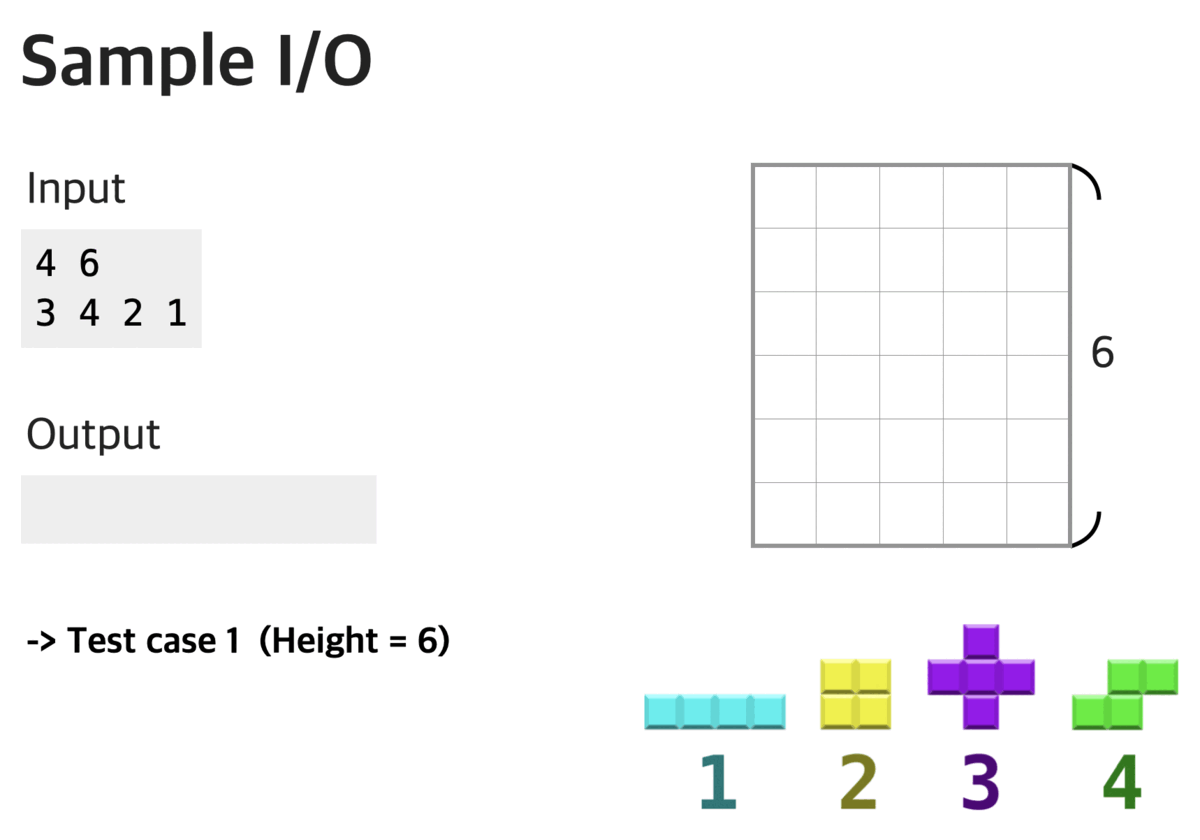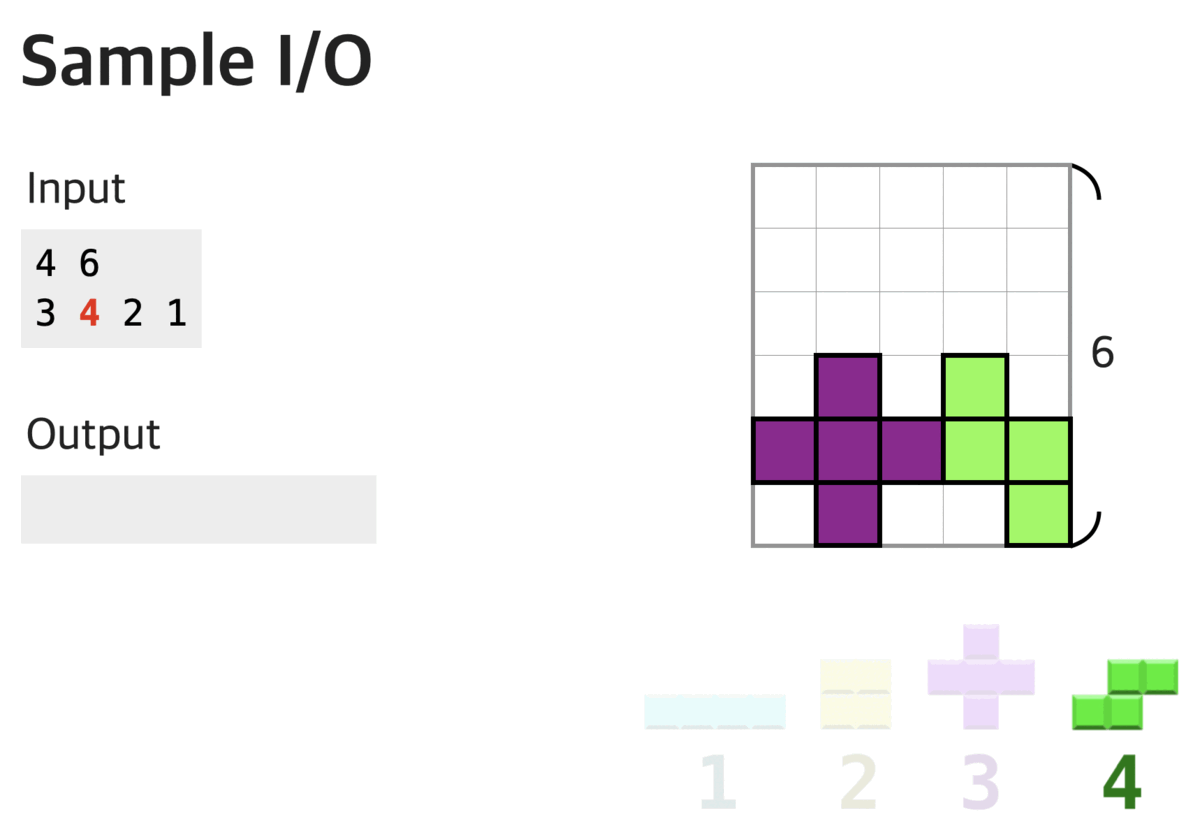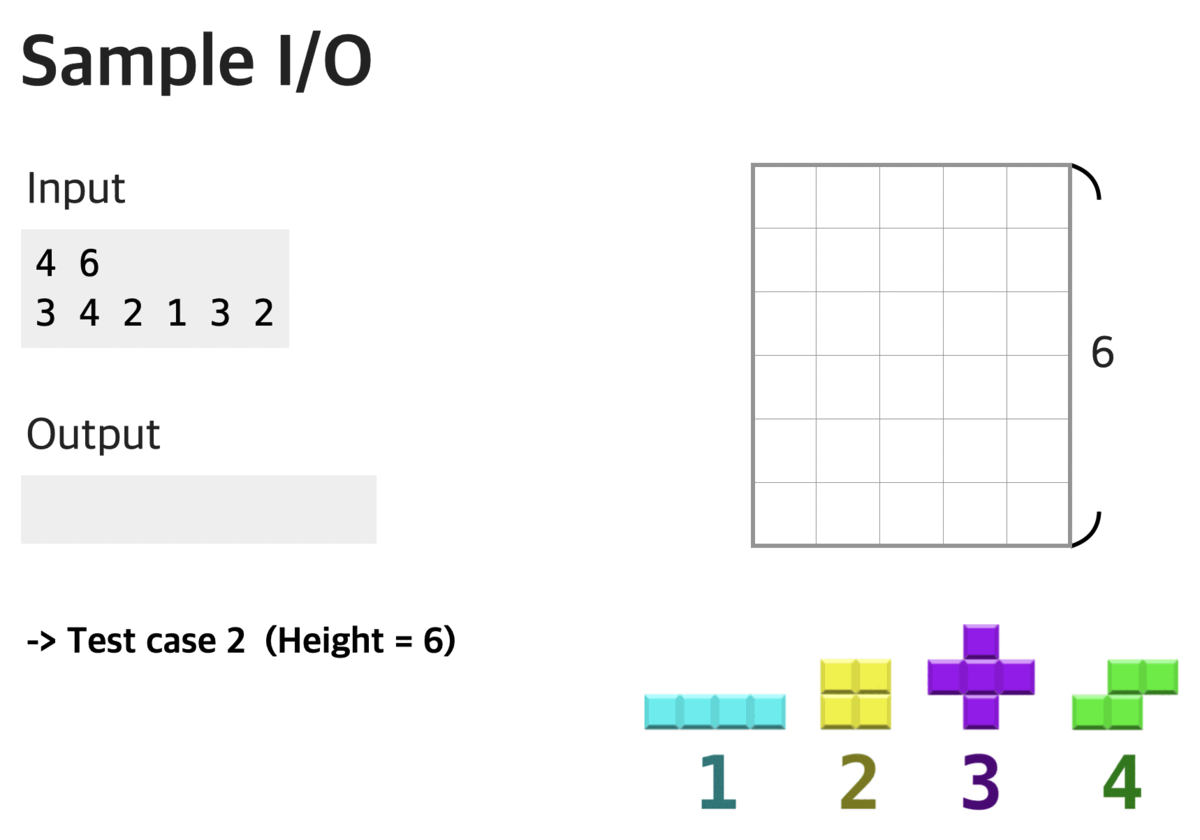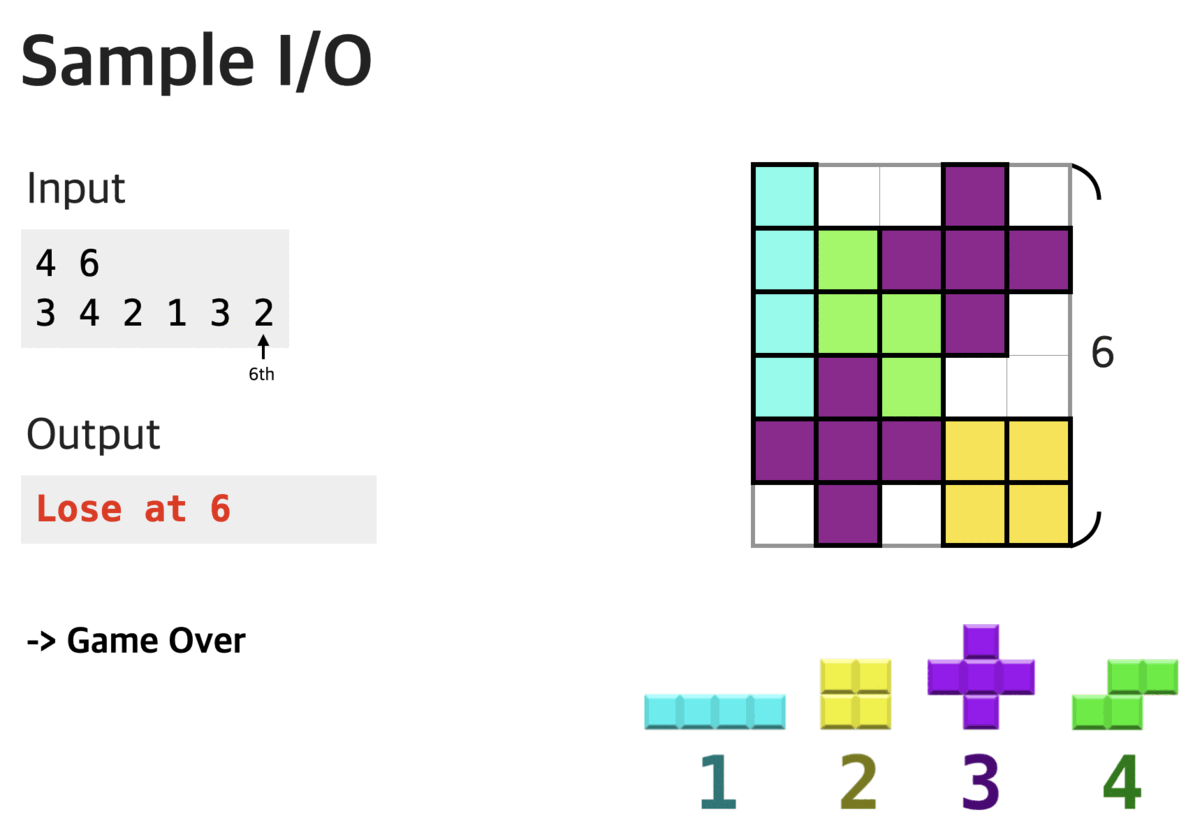
In this problem, we want to simulate the gaming process of Tetris, and several rules differ from the original Tetris:
- The playing field width is 5, and we have only four types of tetromino shapes.
- When the tetrominoes form a horizontal line, the line won't be disappeared but remains in the same place.
- You can only rotate the tetrominoes before you drop them into the field; you must decide the directions of the tetrominoes first and choose the place you want to put them in. The tetromino would fall until it touches the ground or the other tetrominoes.
The following figure shows the four types of tetrominoes.

Given a sequence of the tetromino type, you must put it into the playing field by order.
If we put a tetromino into the field that the height of the stacked tetromino would exceed the top of the playing field, then the game would fail. In this problem, you only need to determine whether the game will end successfully; we can put all the tetrominoes into the field, and no tetromino exceeds the top of the playing field. (Notice: exactly reaching the top is acceptable in this problem)
If the game failed in the end, tell the game would end at x-th tetromino. Since we want to maximize the possible game time, please output the largest x.
Input
The first line contains a positive integer T ≦ 10, representing the number of test cases.
For each test case:
The first line contains two positive integers N, W ≦ 20, representing the tetrominoes' sequence length and the playing field's height.
The second line contains N integers, each a number from 1 to 4, representing the type of each tetromino.
Output
For each test case, output one line.
- If there exists a way that the game would end successfully, print "Win\n".
- Otherwise, the game would end at x-th tetromino, print "Lose at x\n".
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Today, as usual, the cookie monster is picking the cookies to eat for this meal. He is so tired and unable to select the cookies he wants since he was busy preparing for his midterm and didn’t sleep last night. As his good friend, you decided to help him so he doesn’t need to worry about his lunch.
There are n cookies in the shop. For each cookie, there is a number di, representing how yummy the ith cookie is. In general, the larger di is, the more delicious the ith cookie is. However, due to some unknown reasons, the cookie monster especially loves cookies that contain the digit 7 in their di. For example, the digit ‘7’ appears twice in 7927 and appears once in 70. If there are more digits ‘7’ appearing in di for a cookie, the cookie monster would tend to choose that cookie first.
Moreover, here’s your cookie-choosing strategy:
- For any two cookies, always choose the one that with more ‘7’ appears in di first.
- If there are two cookies containing the same amount of ‘7’ in their di, choose the one with larger di.
However, the number di does not directly be marked on the wrapper of the cookie. Instead, there is a string si printed on each wrapper, specifying the value of di. The format of si would be like this:
t1|t2|...|tm, where ti is a number shown in hexadecimal.
And the value of di is the concatenate of all decimal notations of ti, for i = 1, 2, …, m. For example, if si = 2C|4|A, then di = 44410.
Now the cookie monster wants to choose k cookies at most for this meal, help him choose the cookies he is going to eat.
Input
The first line contains two integers n, k, representing the number of cookies in the shop and the amount cookies you are going to choose, respectively.
The next n lines each contains a string, The 1+ith line specifies the value of si.
Constraints:
1 ≤ n ≤ 1000
1 ≤ di ≤ 10300
1 ≤ k ≤ n
1 ≤ ti ≤ 7FFFFFFF16 (= 214748364710)
1 ≤ |si| ≤ 250
Output
Output k lines, the value of di for each cookie you choose, in the order that the smaller value prints first.