| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13015 | Portal maze |
|
| 13018 | Diagonally sorting |
|
| 13020 | Happy B to As with Weeheehea |
|
| 13420 | Domo travels around the world |
|
| 13673 | Domo: When can we go out? |
|
| 13716 | Sebastian Domo |
|
| 13721 | Hints of mid2_practice |
|
Description
There are T tasks you have to solve. In each task, you are given a maze which is a n x m grid. Each cell is marked exactly one character. In the begining, you are at starting point. You need to answer whether it's possible to go to destination. Here are the rules:
- The cell marked '$' is starting point and the cell marked '&' is destination. There must be exactly one starting point and exactly one destination.
- The cell marked '#' is wall, you cannot be at that cell.
- Suppose you are at the cell (i, j), you can go to adjacent cell(i.e (i-1, j), (i, j-1), (i, j+1) and (i+1, j)) if the cell you want to go is not out of bounds and is not marked as '#'.
- If you are at the cell marked lower case letter, you will be send to the cell marked in corresponding upper case letter. But not vice versa. That is if you are at the cell marked upper case letter, nothing will happen. So you can imagine that they are one-way portal. For every existing lower case letter, there must be exactly one corresponding upper case letter. And vice versa.
The folloing show how to go to destination for the first and the third task in Sample.
$b.#. $a.#.
...#B ...#A
...## #..#.
##..& ...#&
.#.#.
-the first task -the third task
Note: be carefule of the efficiency of your strategy.
Input
The first line contains an integer T (1 ≤ T ≤ 10) – the number of tasks you have to solve.
For each task, first there are two integers N, M (2 ≤ N, M ≤ 300) – the gridsize of the maze. Then following N lines contain M characters each, the j-th element in the i-th line Sij is the character marked for the (i, j) cell(Sij must be '$' or '&' or '#' or '.' or letter).
Output
For each task output "Yes" if it's possible to go to destination. Otherwise output "No". Then print a newline('\n').
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given a NxM array, please sort each diagonal line in ascending order from top-left to bottom-right.
For example, given 4x4 array, you should sort these diagonal lines:
This problem is partial judge, you need to implement the function:
// Sort each diagonal line of arr (which size is row x col)
void array2d_sort(int row, int col, long long arr[][500]);
Input
The first line contains two integers, N, M.
The next N lines contain the array, each element in the array is separated by a space.
1 ≤ N, M ≤ 500
-1010 ≤ element in the array ≤ 1010
Output
Output the diagonally sorted array, with each element in the array separated by a space, and print out a newline after each row.
Sample Input Download
Sample Output Download
Partial Judge Code
13018.cPartial Judge Header
13018.hTags
Discuss
Description
Let's call a grid 8-puzzle board if the gridsize is 3 x 3 and there is exactly one cell is 'x' and others are '1' or '0'.
In one operation, you can exchange the 'x' cell of a 8-puzzle board with any cell which is adjacent to the 'x' cell. The cell (i, j) is adjacent to the cell (i-1, j), (i, j-1), (i, j+1) and (i+1, j) (if not out of bounds).
Now you are given N + 1 8-puzzle boards A1, A2, ..., AN and B. You need to answer how many 8-puzzle boards of A1, A2, ..., AN could be made into B in at most K operations.
Sample Explanation
Here are the N + 1 8-puzzle boards A1, A2, ..., AN and B of sample, where N = 4, K = 2.
0 x 0 0 0 0 0 0 0 0 0 1 0 x 0
1 0 1 1 x 1 0 1 1 1 0 x 1 0 1
0 0 1 0 0 1 x 0 1 0 0 1 0 0 1
A1 A2 A3 A4 B
A1, A2 and A4 could be made into B in K operations. The following show some feasible way to make them into B.
A way to make A1 into B in K operations:
0 x 0
1 0 1
0 0 1
A1 is as same as B in the beginning
A way to make A2 into B in K operations:
0 0 0 0 x 0
1 x 1 ========> 1 0 1
0 0 1 0 0 1
exchange (1,2)
A way to make A4 into B in K operations:
0 0 1 0 0 x 0 x 0
1 0 x ========> 1 0 1 ========> 1 0 1
0 0 1 0 0 1 0 0 1
exchange (1,3) exchange (1,2)
Input
The first line contains two integers N and K – the number of 8-puzzle boards in A and the maximum number of operations you can execute for each 8-puzzle board.
Then you are given A1, A2, ..., AN and B in the order. All of them are in 3 lines of 3 characters. Please refer to Sample Input.
It's guaranteed that:
- For testcase 1~6: 1 ≤ N ≤ 10, 0 ≤ K ≤ 7
- For testcase 7: 1 ≤ N ≤ 105, 0 ≤ K ≤ 7
- For testcase 8: 1 ≤ N ≤ 105, 0 ≤ K ≤ 10
To pass testcase 7 and 8, note the efficiency of your strategy(code). It may be a little hard, so maybe you can try to solve other problems first after you pass first six testcases.
Output
Output how many 8-puzzle boards of A1, A2, ..., AN could be made into B in K operations and then print a newline('\n').
Sample Input Download
Sample Output Download
Tags
Discuss
Description

(Domo's friend Kao who gives him the VIP service)
Domo is a brilliant dog, but after this semester, he is very tired and needs to have some rest. Hence, he wants to travel around the world.
Luckily, Domo's friend gives him the VIP service, which can have a flight for free between some cities.
Now, given the number of cities and the free flight list, and Domo starts its travel from the city 0, please find out that how many tickets Domo needs to buy to travel to all the cities (you need 1 ticket to travel from one city to another).
For example, the sample gives 6 cities and 4 pairs of free flights (black line) shown as below:
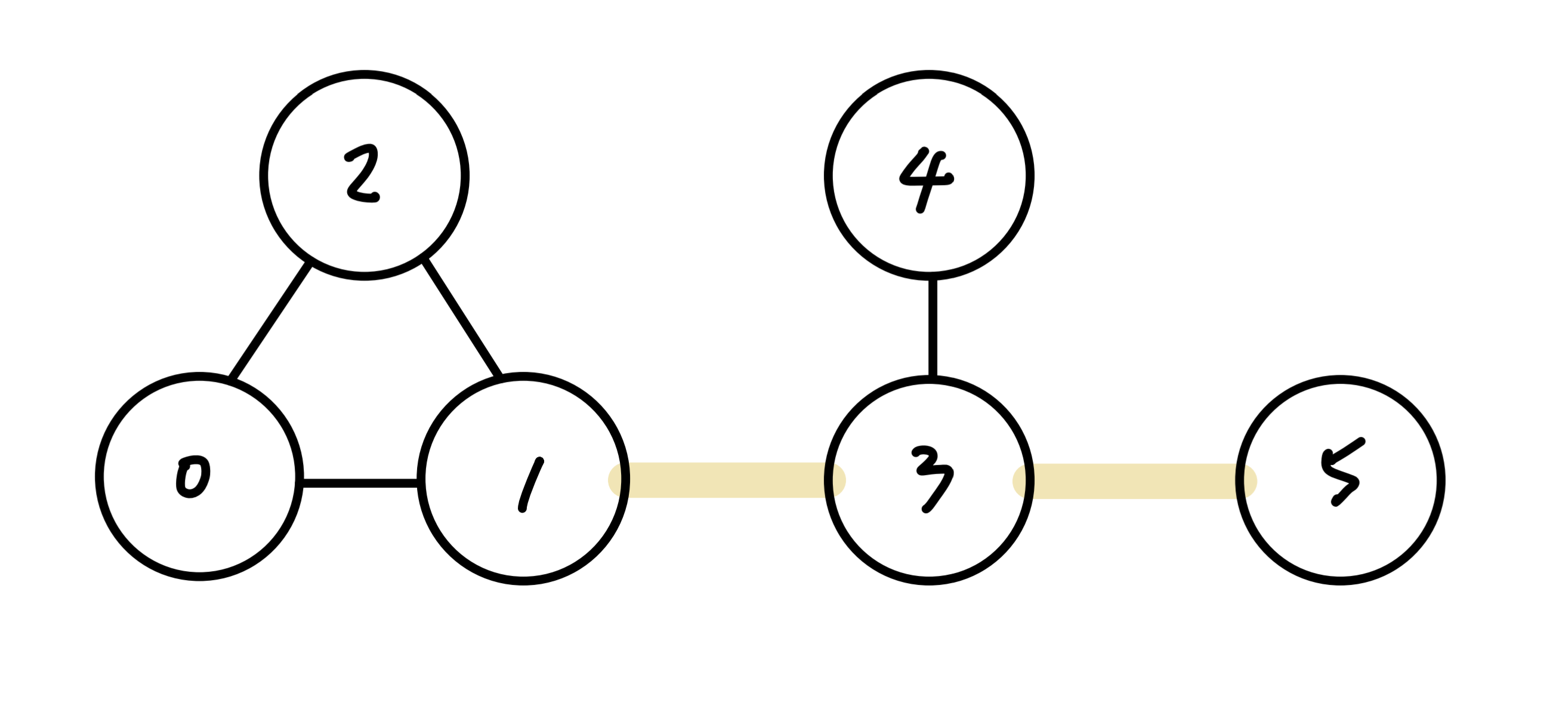
We need at least two tickets to travel to all the cities (for example, from 1 to 3 and from 3 to 5), hence the answer is 2.
There are two hints for this problem:
Hint 1: (You might get 3/6 with this hint)
If there isn't any cycle on the map, we can directly find the answer using the integer N and K.
In other words, you don't need to consider what the graph looks like, since we can list an equation for the answer with the integer N and K.
Hint 2 : (Complete solution. You may solve this problem with this hint)
visit[] // check whether every city has been visited.
count = 0;
while (!visit_all_cities) {
pick_one_unvisited_city(); // pick an unvisited city.
mark_free_cities(); // mark all the cities we can travel from this city without any ticket.
count++; // increase the group count.
}
ans = ? // find out the relation between the answer and the group count!
Input
The first line consists of two numbers N (1 ≤ N ≤ 100) and K (1 ≤ K ≤ N⋅(N-1)/2) - denoting that there are N cities in the world.
For the next K lines, each line contains two numbers A, B (0 ≤ A, B < N) - denoting that Domo can have a free flight between A and B (A ↔ B).
Output
Print the minimum number of tickets that Domo needs to buy to travel around all the cities.
Remember to print an '\n' at the end of the line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Domo is a brilliant dog. This day, he is sitting on the table and waiting for you to take him for a walk.
To finish your job, please find out the total number of blocks you need to fill to get the perfect image you want.
Given an integer N and a string S, we can generate an image with a width and height that are both 2N as below:
(1) if S == "1", we will fill all the blocks.
(2) if S == "0", all the blocks will remain empty.
(3) if S == "2StlStrSblSbr", we will divide the image into 4 squares with a width and height that are both 2N-1, where Stl, Str, Sbl, and Sbr are strings that generate the image of corresponding squares. (Stl generates the image of the top-left square, Str generates the image of the top-right square, and so on).
For example, if N = 2 and S = "20100", the image will be:
There's another example, if N = 3 and S = "221010011", the image will be:
Please find out the total blocks you need to fill. Furthermore, if the given S is invalid (i.e. S cannot generate the corresponding image), please output "Domo".
Once you solved this problem, please take Domo for a walk before dinner time!
Input
The input contains an integer N and a string S, where S only contains characters '0', '1', and '2'.
(1 ≤ N ≤ 5, 1 ≤ length(S) ≤ 20)
Output
Output the number of blocks you need to fill, or "Domo" if S cannot generate an image.
Note that you don't need to print '\n' at the end of the output.
Sample Input Download
Sample Output Download
Tags
Discuss
Description


Sebastian Domo is a Formula One racer. Now it's the last race in Abu Dhabi, he needs this win to get his first world championship.
During this race, he is leading the Grand Prix for 57 laps, there is one more lap to go. However, in the early part of the race, he got a 5-second penalty for causing a collision with others. He needs to finish his race faster than his competitors by at least 5 seconds to win the race.
There is an NxM grid representing the race circuit, where '.' is the track, 'X' is the wall, and '-' is the finish line.
You and your competitors can move on the map in 4 directions (up, left, down, right). Moving one step costs you 1 second. However, you can not move into a wall.
Given the race circuit and the start position of yours and your competitors, please find out whether Domo can win his first world championship, and the difference between your finish time and the fastest competitor's time.
Input
The first line consists of 3 integers N, M, and Q, representing the size of the race circuit, and the number of competitors.
(1 ≤ N, M ≤ 20, 1 ≤ Q ≤ 3)
For the next N lines, each line consists of M characters, representing the race circuit.
For the next Q+1 lines, each line consists of two numbers i and k, representing Domo's position and his competitors' position on which row and which column.
(0 ≤ i < N, 0 ≤ k < M)
During the racing, you don't need to worry about the fighting between Domo and his competitors (moving into the same grid), it won't affect their pace at all.
It's guaranteed that using recursion can solve this problem.
The aligned sample input
Output
Output the time Domo and his competitors need to finish the race at the first line, separated with whitespaces.
At the second line, output the finish time difference between Domo and the fastest competitor.
Remember to print a newline character at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
To help you finish these problems before the midterm, here's the recommended order to solve problems. But you can still have your own solving order.
Easy: [13018, 13420]
Medium: [13015, 13020, 13673]
Hard: [13716]
Techniques may be used in problems:
13015: DFS
13018: sort method (bubble sort, insertion sort, qsort, etc.)
13020: recursion
13420: DFS
13673: recursion
13716: BFS (Problem has been designed well so DFS is also acceptable)
About DFS and BFS: