| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11213 | permutations |
|
| 13689 | Doracarpet |
|
Description
Given a set of n≧1 elements, the problem is to print all possible permutations of this set. For example, if the set is (1,2,3), then the set of permutations is {(1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,2,1), (3,1,2)}.
<Hint1>
Looking at the case of four elements (1,2,3,4). The answer can be constructed by writing
- ‘1’ followed by all the permutations of (2,3,4)
- ‘2’ followed by all the permutations of (1,3,4)
- ‘3’ followed by all the permutations of (1,2,4)
- ‘4’ followed by all the permutations of (1,2,3)
<Hint2>
A recursive method to implement the above idea is as follows:
Consider the case of (1,2,3,4), that is, n=4.
- Place the set elements in a global array, and set the position index “k” as 0.
- Use a for-loop to “swap” (or exchange) the 1st element with the 1st element, the 2nd element, the 3rd element, and the 4thelement, respectively.
- In each loop-iteration:
- increment the position index “k” by 1 (for considering only the remaining elements in the following recursive call);
- use the updated k to recursively call your permutation function;
- note that because you use a global array, remember to swap back the two elements after the iteration.
- In each loop-iteration:
- In a recursive-call path, when k reaches n, it means that you get a possible permutation.
You will be provided with the following sample code, and asked to implement function "Swap" and "Perm.
#include <stdio.h>
char list[10];
void show(int n)
{
int i;
printf("(%c", list[0]);
for (i=1; i<n; i++) {
printf(",%c", list[i]);
}
printf(")\n");
}
void Swap(int k, int i)
{
/*your code*/
}
void Perm(int k, int n)
{
/*your code*/
}
int main(void)
{
int num, i;
scanf("%d", &num);
for(i=0; i<num; i++)
list[i] = '1'+i;
Perm(0, num);
return 0;
}
Input
The decimal number n that represents the number of elements in the set.
(1≦n≦5)
Output
In the output you should print all the permutations.
Be sure to add a newline character '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Doraemon loves programming and overcomplicating things. Today, he wants to make a new carpet for Nobita's house, so he use his programming skill to design a cool pattern for the new carpet, and call it the "doracarpet"!
To have the carpet to be fit in all the rooms, we need it to be in a different size. The following are the rules of pattern for each size of the doracarpet, and we define a size-x doracarpet would be a square carpet with a side length equal to 4×2x-1, for example, a size-4 doracarpet is a square with a side length of 32.
The following is what the doracarpet in each size looks like:
Size-1 doracarpet looks like a plus sign.

Size-2 doracarpet is made of four size-1 doracarpet and arranged like the following figure.

Size-3 doracarpet, has a size-2 doracarpet in the center, and put four U shapes in four different directions and it looks like the following figure.
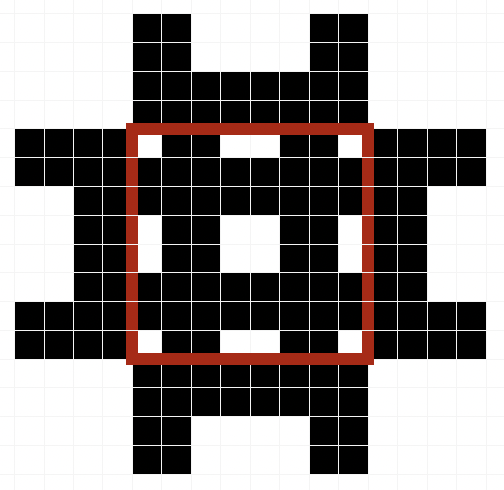
Size-4 doracarpet is made of four size-3 doracarpet and arranged like the following figure.

Size-5 doracarpet, has a size-4 doracarpet in the center, and put four U shapes in four different directions and it looks like the following figure.
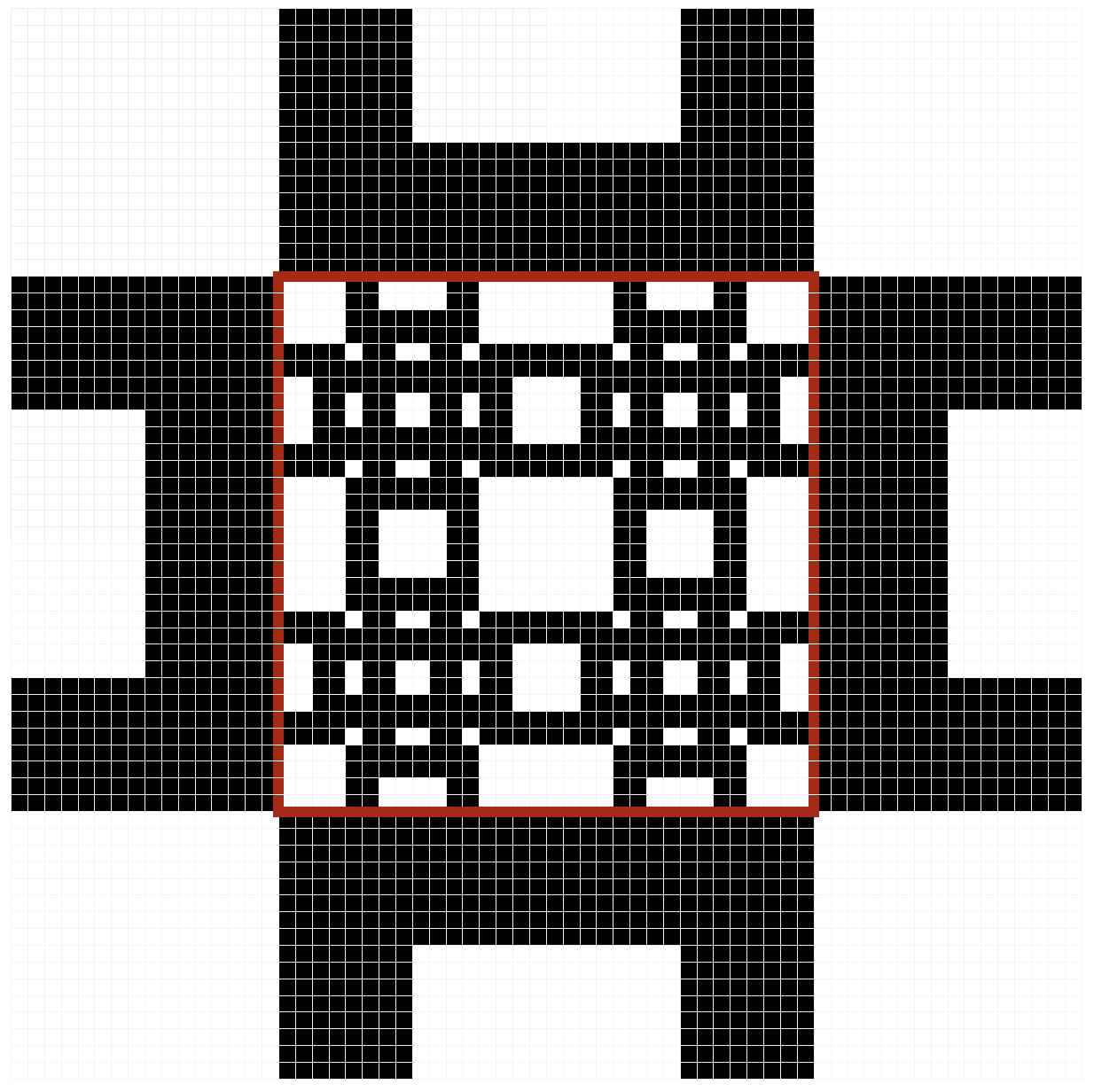
So we discover that when x > 1, and:
- If we have a size-x doracarpet with x % 2 == 0, it would be made of four size-(x-1) doracarpet.
- If we have a size x doracarpet with x % 2 == 1, we would have a size-(x-1) doracarpet in the center and put four U shapes in four different directions.
Input
The input contains only an integer x, with 0 < x < 12.
Output
Output what a size-x doracarpet looks like, use '#' and '.' to represent the black and white block of it.
You may refer to the sample IO to know how to print the result, and don't forget to print a '\n' at the last line.