| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11213 | permutations |
|
| 12459 | Sierpinski Carpet |
|
| 12991 | Toad Jumping |
|
Description
Given a set of n≧1 elements, the problem is to print all possible permutations of this set. For example, if the set is (1,2,3), then the set of permutations is {(1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,2,1), (3,1,2)}.
<Hint1>
Looking at the case of four elements (1,2,3,4). The answer can be constructed by writing
- ‘1’ followed by all the permutations of (2,3,4)
- ‘2’ followed by all the permutations of (1,3,4)
- ‘3’ followed by all the permutations of (1,2,4)
- ‘4’ followed by all the permutations of (1,2,3)
<Hint2>
A recursive method to implement the above idea is as follows:
Consider the case of (1,2,3,4), that is, n=4.
- Place the set elements in a global array, and set the position index “k” as 0.
- Use a for-loop to “swap” (or exchange) the 1st element with the 1st element, the 2nd element, the 3rd element, and the 4thelement, respectively.
- In each loop-iteration:
- increment the position index “k” by 1 (for considering only the remaining elements in the following recursive call);
- use the updated k to recursively call your permutation function;
- note that because you use a global array, remember to swap back the two elements after the iteration.
- In each loop-iteration:
- In a recursive-call path, when k reaches n, it means that you get a possible permutation.
You will be provided with the following sample code, and asked to implement function "Swap" and "Perm.
#include <stdio.h>
char list[10];
void show(int n)
{
int i;
printf("(%c", list[0]);
for (i=1; i<n; i++) {
printf(",%c", list[i]);
}
printf(")\n");
}
void Swap(int k, int i)
{
/*your code*/
}
void Perm(int k, int n)
{
/*your code*/
}
int main(void)
{
int num, i;
scanf("%d", &num);
for(i=0; i<num; i++)
list[i] = '1'+i;
Perm(0, num);
return 0;
}
Input
The decimal number n that represents the number of elements in the set.
(1≦n≦5)
Output
In the output you should print all the permutations.
Be sure to add a newline character '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
This is a Sierpinski Carpet.

The construction of a Sierpinski Carpet is stated as follows. Initially, you are given a white square.
-
Divide the square into nine subsquares in a 3-by-3 grid.
-
Color the center subsquare with black.
-
For the rest eight subsquare, repeat step 1
For example,

Initially (after zero iteration), there is 0 black square in the Sierpinski Carpet.
After one iteration, there is 1 black square in the Sierpinski Carpet.
After two iterations, there are 9 black squares in the Sierpinski Carpet.
After three iterations, there are 73 black squares in the Sierpinski Carpet
Given an integer k, please output number of black squares after k iterations.
Maybe Useless Hint
-
It is suggested to solve this problem using recursion. (Well ... there is mathematic solution, but hope you practice how to design recursion function)
-
Be careful with overflow. Suggest to calculate with long long int.
Input
Input contain a single integer k.
Since there will be overflow issue if k is too big, so in this problem 0 <= k < 10.
Output
Output the number of black squares after the k-th iteration.
Note that there is a newline character after the output.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There are N stones on the river. The height of the i-th stone is hi for 1 <= i <= N and is colored with color ci. Toad Epep is on the S-th stone (where the leftmost stone is the 1-st stone) and he wants to go the the T-th stone with several jumps.
For each jump from the i-th stone, Epep can jump to the (i-1)-th stone (if it exists), the (i+1)-th stone (if it exists), or any stone colored with the same color ci (if it exists).
Epep will only visit each stone at most once. That is, if Epep jumped to the k-th stone at some time, he won't jumped to the k-th stone again.
The energy cost of jump from i-th to j-th stone is |i-j| x |hi - hj|.
Because Epep ate too much insects and wants to do more exercise, can you help Epep to find the way that cost the most energy (if there are several ways with same maximum energy cost, find the way with maximum jumps) ?
Explanation of Sample IO
All possible moves are listed in the following:
-
2 -> 1 -> 4 -> 3 -> 6 -> 5, which costs 100 energy and 5 jumps
-
2 -> 1-> 4 -> 5, which costs 60 energy and 3 jumps
-
2 -> 3-> 4-> 5, which costs 40 energy and 3 jumps
-
2 -> 3 -> 6 -> 5, which costs 40 energy and 3 jumps
-
2 -> 5, which costs 0 energy and 1 jump
Hint:
1. In this problem, you may need to use an array int jumped[N+1] to record whether a stone i has been visited in the currently expanded path.
2. However, you need to manipulate the int jumped[N+1] array properly as follows:
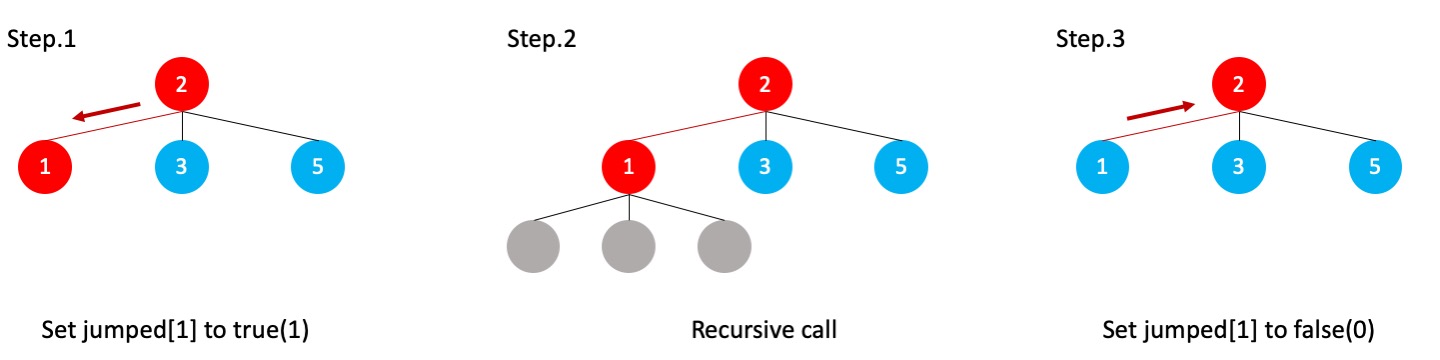
Input
Integers N, S, T are on the first line.
h1, ..., hN are on the second line.
c1, ..., cN are on the third line.
-
1 <= N <= 15
-
1 <= S, T <= N and S != T
-
1 <= hi <= 100000
-
1 <= ci <= 15
Test case description
-
Test case 1: all stones have different colors
-
Test case 2: all stones have the same color
-
The remaining test cases: no additional restrictions
Output
Output two integers E and J, where E is the maximum energy cost and J is the number of jumps in one line. Remember to add \n in the end.