| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11200 | Tower of Hanoi |
|
| 13690 | Bad Fibonacci's soup |
|
Description
The Tower of Hanoi is a mathematical game puzzle. It consists of three rods, which are A, B and C. The puzzle starts with n disks in ascending order of size on rod A, the smallest at the top.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.
Write a program to simulate the moves of the disks. Print the number of disk which is moved in each step.
For example, if n = 3, the moves of each steps are:
move disk 1 from rod A to rod C
move disk 2 from rod A to rod B
move disk 1 from rod C to rod B
move disk 3 from rod A to rod C
move disk 1 from rod B to rod A
move disk 2 from rod B to rod C
move disk 1 from rod A to rod C
You should print out:
1
2
1
3
1
2
1
HINT : You can modify this sample code and implement the function 'hanoi'
#include <stdio.h>
void hanoi(int n, char A, char B, char C);
int main(){
int n;
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
Input
An integer n (0<n<20), which means the number of disk.
Output
Print out the number of disk which is moved in each step, and there is a '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Fibonacci's soup is one of the most well-known recipe in Fibonacci's hometown. Besides making soup, Fibonacci also enjoys seeking weird sequences.
We all know that we would not like to add two days before yesterday's soup into Fibonacci's soup, otherwise, It would cause food safety issues, and it would become "Bad Fibonacci's soup", aka "BFS".
One day, Fibonacci found a new sequence again. Since Fibonacci just eat Bad Fibonacci's soup for his lunch and was vomiting, he decided to name this newly found sequence "Bad Fibonacci's sequence".
The following is the formula for the sequence:
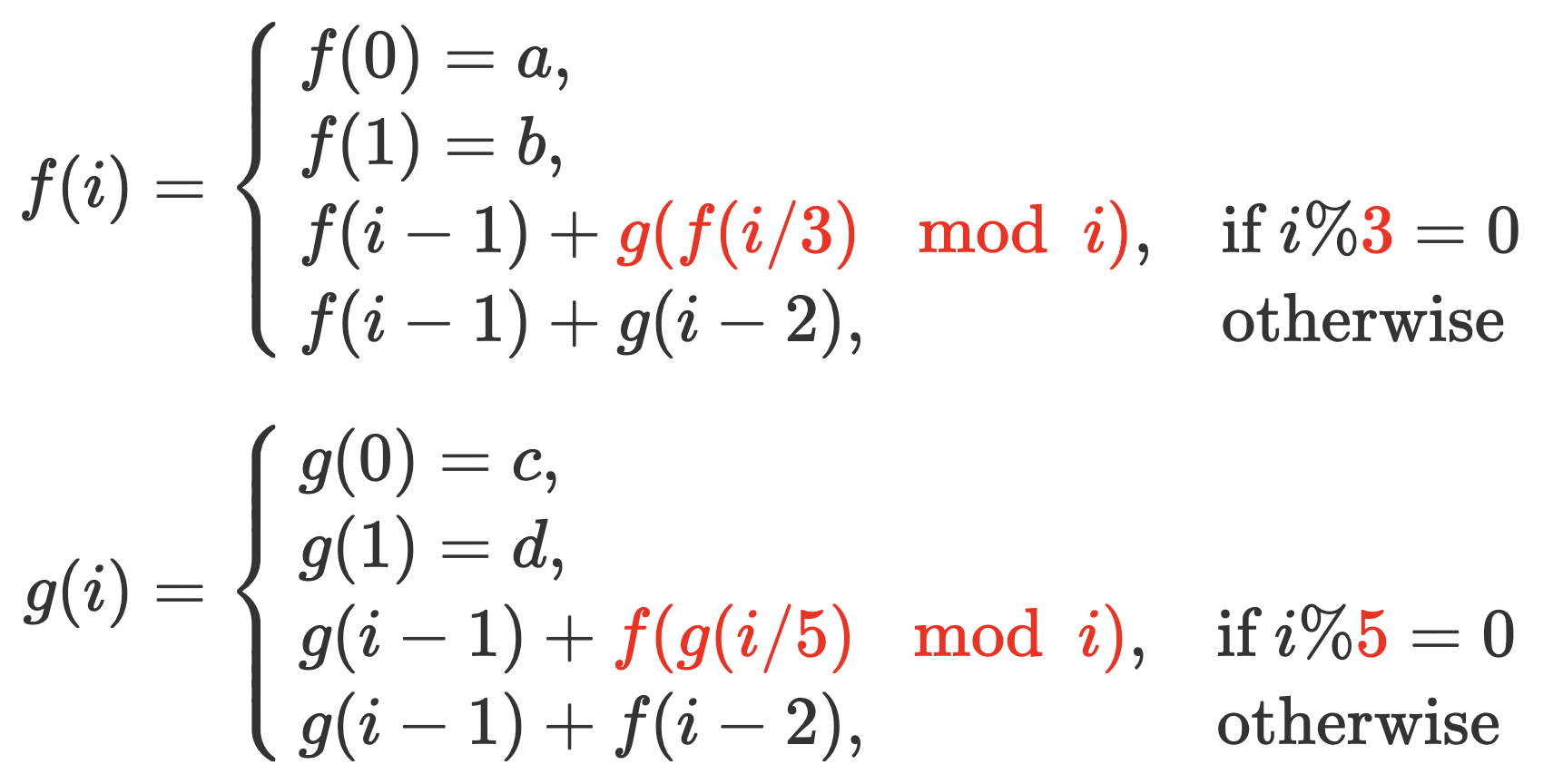
Hint:
If your program gets a "Time Limit Exceeded", your program may solve a same problem (e.g., f(m) or g(n)) too many times. We suggest that you use the dynamic programming method as follows:
- Use a global array to store the solutions to the problems that have been solved so far.
- Then, whenever we attempt to solve a problem, we first check the array to see if the problem is already solved.
- If a solution has been recorded, we can use it directly (that is, no further recursive calls).
- Otherwise, we solve the problem and record its solution in the array.
In this way, we can avoid repeated computation and reduce the computation time significantly.
Input
The input contains one line: nonnegative integers a, b, c, d and n.
Testcase constraints
- For all the testcases: a, b, c, d ≤ 100
- Testcase 1~3: n ≤ 40
- Testcase 4~7: n ≤ 60
- Testcase 8~10: n ≤ 80
Output
Output one line, including f(n) and g(n).
Please remember to print '\n' at the end.