| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11711 | Dynamic 3D array |
|
| 12498 | Partial Judge Example |
|
| 13342 | Domo to omoD |
|
| 13631 | Nugget Frenzy |
|
Description
In this problem, you are asked to design two functions
1.
unsigned*** new_3d_array(unsigned n,unsigned m,unsigned k);
malloc an n*m*k 3D unsigned array, and then return its address. The main function will check the correctness of your array.
2.
void delete_3d_array(unsigned ***arr);
Free the memory space of your array that was previously allocated by using malloc. Be careful about the memory uage of your program allocated dynamically so as to avoid MLE.
The two functions have been declared in function.h, and you are asked to complete the function definitions in function.c.
Your program should construct the 3D array by using only three malloc function calls. Notice that malloc is a time-consuming operation.
Note: for OJ submission:
Step 1. Submit only your function.c into the submission block. (Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
Please refer to the main function.
The input only has one line, consisting of five positive integers t,n,m,k,r separated by space characters, where t is the number of tests, (n,m,k) represents the array size, and r is a parameter for testing.
Note that n*m*k<=10000000 and t*n*m*k<=60000000
Output
In order to test your array's correctness, we will use your array to do some computations and output the results.
Sample Input Download
Sample Output Download
Partial Judge Code
11711.cPartial Judge Header
11711.hTags
Discuss
Description
This is the partial judge example (another method for online judge), you are asked to design a function below:
int call_add(int a, int b);
(implement a function to add two pass value togeter)
Note: for OJ partial judge submission:
Step 1. Submit only your function.c into the submission block. (Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
/* the content below is what you need to copy and submit to oj*/
int call_add(int a, int b){
return a + b;
}
More information about the different of partial judge and normal judge
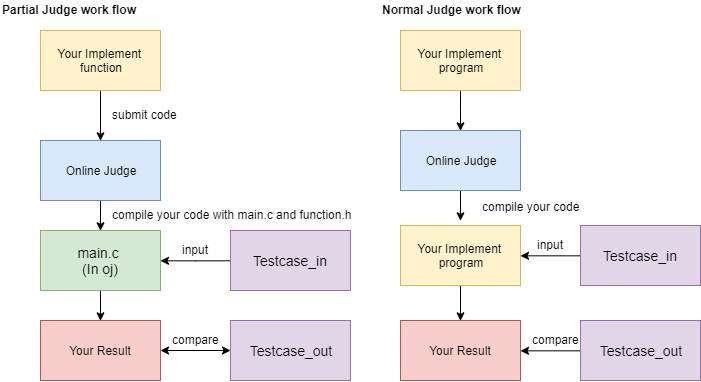
Input
Please refer to the main function.
The input only one line, contain two number a and b (1 < a < 10, 1< b < 10)
Output
Output a + b.
Sample Input Download
Sample Output Download
Partial Judge Code
12498.cPartial Judge Header
12498.hTags
Discuss
Description

Domo is a brilliant dog. When he gets enough sleep, he will be happy.
Unfortunately, he got some problems with his homework this evening. He mistakes 'postfix' as 'prefix', which makes him can't go to sleep until he corrects his homework.
Given a prefix expression, please convert it to the postfix expression or Domo will be punished since he didn't finish his homework.
Prefix: The operator appears in the expression before the operands. Simply of the form (operator operand1 operand2).
Postfix: The operator appears in the expression after the operands. Simply of the form (operand1 operand2 operator).
Take an Example: (A+B) * (C-D)
Prefix: * + A B - C D
Postfix: A B + C D - *
This problem is testing your recursion skill, so don't consider if the expression is valid or not (such as divided by zero)
Input
The first line contains a prefix expression, in which each element is separated with a blank.
It's guaranteed that the number of elements will not exceed 500.
Output
Print the corresponding postfix expression from the given prefix expression, and separate each element with a blank.
You don't need to print a newline character in this problem, I apologize for any inconvenience.
Remember to print a newline character at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Kiara is a fast food shop owner. Today, she made too many chicken nuggets. She only has boxes with k different sizes that can contain a1, a2, … ak nuggets respectively. She wants to put all n nuggets into boxes without any excess nuggets. Please help her determine how many ways she can pack the nuggets.
For example, if she has 14 nuggets and boxes of 3 sizes: for 2, 3, and 4 nuggets, there would be 8 ways to pack the nuggets.

Input
The first line contains two positive integers n and k. (1 ≤ n ≤ 107, 1 ≤ k ≤ 20)
The following line contains k numbers, the number of nuggets that could be packed inside each box. It is guaranteed to be in a strictly increasing order between 1 and n, which means 1 ≤ a1 < a2 < a3 < ... < an ≤ n.
Output
The number of the way to pack the nuggets without any leftovers. Please print a '\n' character at the end.