| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13685 | Hot-Cross-Bun |
|
| 13680 | Mr Bean |
|
Description
Little kai loves to eat hot cross buns as treats, but his mama gave him donuts instead.

There's a n x m grid, in each gridij there is exactly one treat; a donut, 'o' or a hot cross bun, 'x'.
If the treat on gridij is a donut, 'o' , you can change it to a hot cross bun, 'x'. ('o' -> 'x') and vice versa.
And all the other treat inside the grid (i-1, j), (i, j-1), (i, j+1) and (i+1, j) will also be changed. Just like the shape of a hot cross bun !

Mama gave little kai an initial grid of random treats, help little kai find out the minimum number of treats he need to change until all the treats are turned into hot cross buns.
For example, consider a 3 x 3 grid and the treats on (1, 3), (3, 2), (3,3) are hot cross buns in the beginning. The optimal choice to change the treats on (1, 1), (3, 2) and (3, 3).
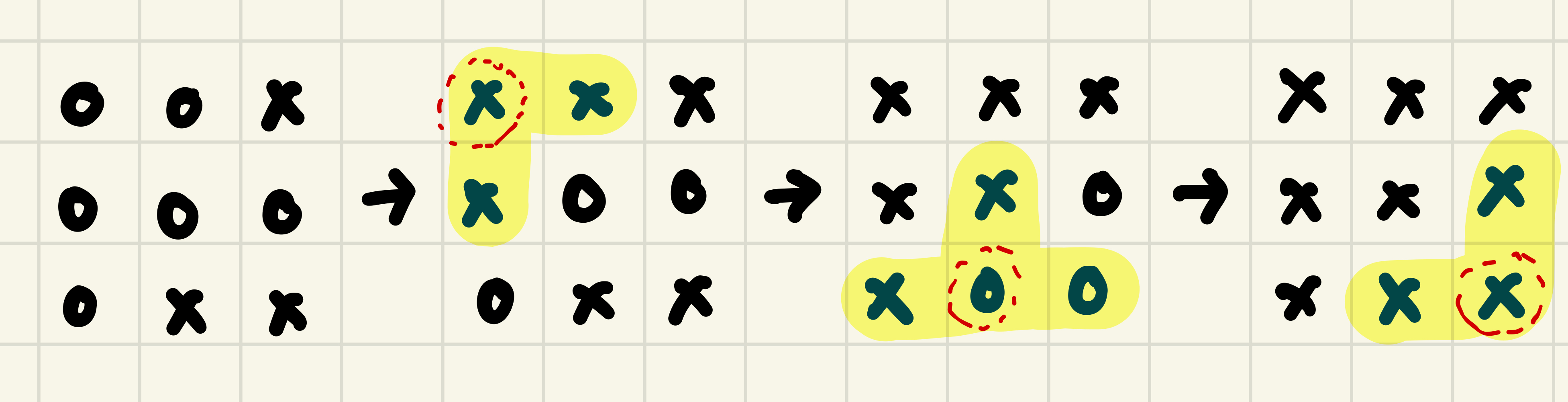
Click here to listen to hot cross bun.
Input
The first line contains two integers n, m ,the grid size
The following n lines contain m characters each, the j-th element in the i+1-th line sij is state where
'x' represents buns and 'o' represents donuts
1 ≤ n x m ≤ 20
Output
Print the minimum number of treats thath little kai need to change until all the treats are turned into hot cross buns.
If there is no solution, print "no solution".
Don't forget to print ('\n').
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Mr Bean likes to play chess,

He likes the queen piece the most because it can move in every direction.
Every grid in the chessboard has an integer X on it. For every queen he places on the chessboard, he gets X points.
He wants to place 8 queens on the chessboard such that no queen threatens one another , where each row and collumn and diagonal of the board contains exactly one queen.
And the sum of the numbers on the chessboard selected is the minimum.
Input
The first line contains one integer K the number of boards.
The following 8 lines contain 8 integers each, where each element is Xij
1 ≤ K ≤ 20
0 ≤ Xij ≤ 10000
Output
Print the minimum points.
Dont forget to put newline character.