| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13657 | Escape From the Maze |
|
| 12486 | Tower of Hanoi |
|
Description
One day, you find out that you are trapped in a maze. While panicking, you see a mini map in front of you.
Unfortunately, you are still not sure if you can escape from this maze or not, and so, what you need to do is to determine whether you can reach the destination of this maze or not !
You can only move left, right, up, and down (diagonal move is not acceptable) !
The mini map is a size m x n matrix, and it consists of four symbols:
'.' is the road you can walk through.
'x' is the wall that you can not walk through.
'S' is the the starting point.
'D' is the destination you want to reach.
Your goal is to find whether there exists a path from the starting point S to destination D.
For example, a 4 x 5 map will look like:
D . . . .
x x x x .
x x x x .
S . . . .
(There is a space in front of each charactor!)
Input
There will be 3 parts of input.
(1) The first line contains two integers m, n, which is length and width of the map (1 ≤ m, n ≤ 1000)
(2) The second line is a positive integer T, which is the number of testcases.
(3) There areT amounts of m*n mini map separated by a newline character among each mini map, which contains characters including '.', 'x', 'S', 'D' .
Output
If you can reach the destination, please print "ESCAPE!", otherwise print "QQ".
Note that you need to print a newline character ('\n') at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The Tower of Hanoi is a mathematical game puzzle. It consists of three rods, which are A, B and C. The puzzle starts with n disks in ascending order of size on rod A, the smallest at the top.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.
Write a program to simulate the optimal moves of the disks. Print the number of disk which is moved in each step.
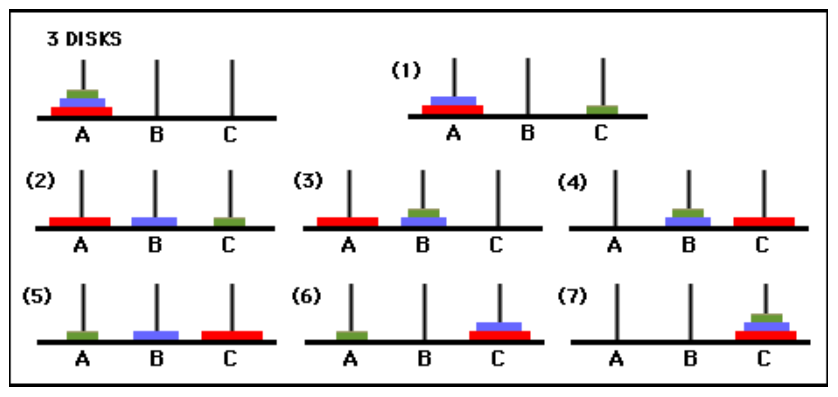
For example, if n = 3, the moves of each steps are:
move disk 1 from rod A to rod C
move disk 2 from rod A to rod B
move disk 1 from rod C to rod B
move disk 3 from rod A to rod C
move disk 1 from rod B to rod A
move disk 2 from rod B to rod C
move disk 1 from rod A to rod C
HINT : You can modify this sample code and implement the function 'hanoi'
#include <stdio.h>
void hanoi(int n, char A, char B, char C);
int main(){
int n;
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
Input
An integer n (0<n<20), which means the number of disk.
Output
Print out the information of each step, and there is a '\n' at the end of each line.
