| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11945 | Treasure Hunting |
|
| 13227 | Yu-Gi-Oh! |
|
| 13231 | cheat sheet |
|
| 13514 | Make it very beautiful |
|
| 13532 | Promenade Dance |
|
Description
Niflheimr is playing Minecraft recently. He occupies a lot of towns, and there are many diamonds inside some of those towns.
Whenever he runs out of diamond, he has to figure out the nearest town with diamonds from his current location.
Doing this task every time waste a lot of time. He asks you to help him for the calculation. For every town, find the shortest distance to get diamonds from a nearby town which has diamonds. If the town itself has diamonds, the distance would be 0.
Hint: Use BFS (Breadth First Search) and std::queue.
If you are not familiar with BFS, you should take a look at the following article:
http://alrightchiu.github.io/SecondRound/graph-breadth-first-searchbfsguang-du-you-xian-sou-xun.html
[IMPORTANT] For those almost run out of time, maybe this note can help you figure out BFS and solve this problem faster!
You are provided with the following code:
#include <queue>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// G[i] is the neighbor towns of town i
vector<int> diamondTowns;
vector<int> G[100005];
int Dist[100005];
struct node {
int id;
int dist;
node(int id, int l) {
this->id = id;
this->dist = l;
}
};
int main() {
int N, M, K;
cin >> N >> M >> K;
for (int i = 0; i < M; i++) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
G[b].push_back(a);
}
for (int i = 0; i < K; i++) {
int x;
cin >> x;
diamondTowns.push_back(x);
}
fill(Dist, Dist+100005, -1);
queue<node> Q;
// [TODO] complete the task!
// Output
for (int i = 1; i <= N; i++) {
cout << Dist[i] << '\n';
}
return 0;
}
You may take it as reference. You are not required to use this code, though.
Input
First line of input contains three integer N, M, K, denoting the number of towns, the amount of roads between towns and the number of towns which has diamond.
All the towns are numbered from 1 to N.
For the next M lines, each of them contains two integer a, b, meaning there is a road between a and b. All the roads are bidirectional, and the length of these roads are all 1.
The last line of input contains K distinct integers, denoting the towns which has diamonds.
It is guaranteed that:
- 1 <= K <= N <= 105
- 1 <= M <= min(106, N*(N+1)/2)
- All the towns can reach each other, i.e. the graph is connected.
Output
Output consists of N lines.
For i-th line, output the shortest distance Niflheimr has to travel from town i to get a diamond.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Seto Kaiba is a grand master player of Yu-Gi-Oh.
Cards are necessary, and it's why Kaiba buys cards from time to time.
The cards are labeled with numbers.
The card Kaiba has the most is his ace. If there are two or more kinds of cards Kaiba has the most at the same time, the cards with maximum number is Kaiba's ace.
For example,
Buy: 2; Cards in hand: 2; Ace: 2
Buy: 1; Cards in hand: 2 1; Ace: 2 (Becasue 2 is the largest number)
Buy: 1; Cards in hand: 2 1 1; Ace: 1 (Becasue 1 is the most one)
Please find out what Kaiba's ace is whenever he buys a new card.
Input
The first line contains a number N — Kaiba buys N cards in total.
Each of the next N lines contains a number ai — the number of the cards Kaiba buys.
testcase 1 and 2: N <= 100, ai <= 109.
testcase 3 and 4: N <= 3000, ai <= 1018.
testcase 5 and 6: N <= 100000, ai <= 1018.
Output
The output should contains N lines, each of which contains a number — Kaiba's ace.
Remember to add new line at last.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
string:
Strings are objects that represent sequences of characters.
#include <string>
begin: Return iterator to beginning
end: Return iterator to end
rbegin: Return reverse iterator to reverse beginning
rend: Return reverse iterator to reverse end
empty: Test whether container is empty
clear: Clear string
length: Return length of string
substr: Generate substring
push_back: Append character to string
pop_back: Delete last character
set:
Sets are containers that store unique elements following a specific order.
#include <set>
begin: Return iterator to beginning
end: Return iterator to end
rbegin: Return reverse iterator to reverse beginning
rend: Return reverse iterator to reverse end
empty: Test whether container is empty
clear: Clear content
size: Return container size
insert: Insert element
erase: Erase elements
find: Get iterator to element
list:
Lists are sequence containers that allow constant time insert and erase operations anywhere within the sequence, and iteration in both directions.
#include <list>
begin: Return iterator to beginning
end: Return iterator to end
rbegin: Return reverse iterator to reverse beginning
rend: Return reverse iterator to reverse end
empty: Test whether container is empty
clear: Clear content
size: Return container size
front: Access first element
back: Access last element
emplace_front: Construct and insert element at beginning
emplace_back: Construct and insert element at the end
push_front: Insert element at beginning
push_back: Insert element at the end
pop_front: Delete first element
pop_back: Delete last element
vector:
Vectors are sequence containers representing arrays that can change in size.
#include <vector>
begin: Return iterator to beginning
end: Return iterator to end
rbegin: Return reverse iterator to reverse beginning
rend: Return reverse iterator to reverse end
empty: Test whether container is empty
clear: Clear content
size: Return container size
front: Access first element
back: Access last element
emplace_back: Construct and insert element at the end
push_back: Add element at the end
pop_back: Delete last element
queue:
#include <queue>
empty: Test whether container is empty
size: Return container size
push: Insert element
pop: remove next element
front: Access next element
stack:
#include <stack>
empty: Test whether container is empty
size: Return container size
top: Access next element
push: Insert element
pop: remove next element
map:
#include <map>
begin: Return iterator to beginning
end: Return iterator to end
rbegin: Return reverse iterator to reverse beginning
rend: Return reverse iterator to reverse end
empty: Test whether container is empty
clear: Clear content
insert: Insert Element
erase: Erase element
count : Count elements with a specific key
find: Get iterator to element
operator[]: Access element
lower_bound: Return iterator to lower bound
upper_bound: Return iterator to upper bound
deque:
#include <deque>
push_front: Insert element at beginning
push_back: Insert element at the end
pop_front: Delete first element
pop_back: Delete last element
empty: Test whether container is empty
size: Return container size
insert: Insert element
erase: Erase element
operator []: Access element
front: Access first element
back: Access last element
clear: Clear the container
Input
Output
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given a sequence A = a1, a2, ..., aN.
A continuous subsequence A[L ... R] = aL, ..., aR of A is called very beautiful if every element in A[L...R] is unique.
There will be Q queries.
In the i-th query, you'll be given Li and Ri and you have to find the minimum number of elements needed to be removed to make the subsequence A[Li...Ri] very beautiful.
It is guaranteed for each i = 1, 2, ..., Q - 1, Li ≤ Li+1 and Ri ≤ Ri+1.
For example, if A = [1, 3, 3, 4, 1] and L = 1, R = 5.
You can remove A[1] and A[3] to make A very beautiful.
On the other hand, removing one element is not enough to make A very beautiful.
Hence, the minimum number of elements needed to be removed is 2 in this example.
It is recommended to include<stdio.h> and use scanf/printf instead of cin/cout to speed up input and output.
You may need to select c++11, c++14, c++17 as the compiler to avoid compile error.
Input
The first line of the input contains an integer T, the number of testcases.
The first line of each testcase contains two integers N Q, the length of A and the number of queries.
The second line of each testcase contains N integers, a1, a2, ..., aN.
Each of the next Q lines contains two integers Li Ri, the subsequence you are queied.
For each test,
- N ≤ 100, Q ≤ 100
- N ≤ 100, Q ≤ 100
- N ≤ 1000, Q ≤ 1000
- N ≤ 1000, Q ≤ 1000
- N ≤ 200000, Q ≤ 100000
- N ≤ 200000, Q ≤ 100000
T ≤ 10, 1 ≤ ai ≤ 109, 1 ≤ Li ≤ Ri ≤ N.
Output
For each query in each testcase, please print the minimum number of element needed to be removed to make the subsequence very beautiful.
You have to print an extra new line at the end of each testcase, including the last one.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The CS student association held a Christmas party for students with other departments. In the party, each boy invited a girl to be his dance partner. When entering the ballroom, each of them picked up a roll of colored ribbon. The boys then lined up in one single row in the order of their arrival.
Girls then entered the ballroom and picked up the other end of the color ribbon from the boys and stretched the ribbon as they lined up in a parallel row of boys. When everyone was set, there are one row of N boys and the other row of N girls, with N ribbons that paired them.
The party host wanted to select some pairs for the first dance. The host decided to cut off the least number of ribbons to make the remaining ribbons not crisscrossed. Then those pairs were selected. In the below example, 4 pairs were selected for the first dance by way of cutting off 2 ribbons. Note that 4 pairs is also the maximum that can be achieved in the example. Given different arrival configurations, your task is to the maximum pairs could be selected for the first dance.
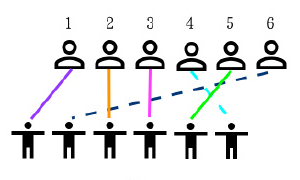
Hint
Look at the figure above. The above row are boys where \(i=0,1,2,3,4,5\), while the below row are girls, where \(a_i=0,5,1,2,4,3\).
First it's obvious for us to observe that if we select girl \(a_i\) (e.g. \(a_2=5\)), then we couldn't select greater \(a_i\) afterwards since it would result in crisscross. That is, we must always select some increasing ones.
Furthermore, to find the answer of this problem, we could rather find all the answers that the last girl we select is \(a_i\). In this way, we have that it is the maximum of the answers of girls before and less than her.
Eventually, for any boy \(i\), if \(\exists j, a_j<a_i\) and the answer of \(a_j\) is less than \(a_i\), then we would never select \(a_i\). Again, the ones we select always increasing.
Input
For each test case, the first line contains one integer, \(N\), where \(N<10^6\), indicating the number of boys. The second line contains \(N\) distinct integers, ranged from \(0\) to \(N-1\). The first integer \(i\) menas that the first boy invited the \(i^{th}\) girl to dance and so on.
In \(40\%\) of test cases, \(N<5000\). In \(20\%\) of test cases, \(N<200\).
Output
Print out the number of pairs selected for the first dance. Remember to print a newline character at the end.