Description

If you are not familiar with partial judge , please check this handout

---

A. Definition of Binary Search Trees

A binary search tree (BST) is a binary tree, whose internal nodes each store a key and each have two sub-trees, commonly denoted left and right. The tree additionally satisfies the property: the key in each node must be greater than all keys stored in the left sub-tree, and smaller than all keys in the right sub-tree.

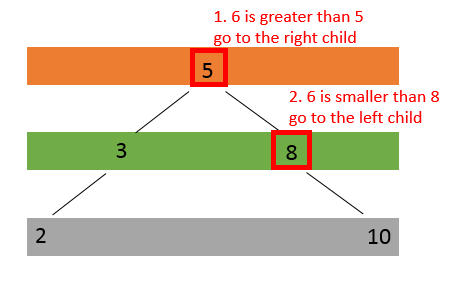
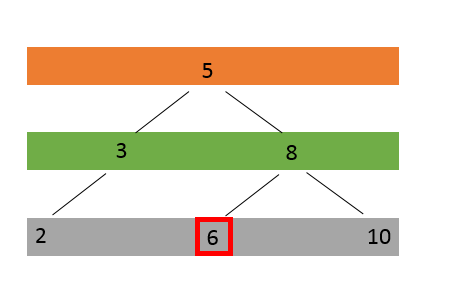
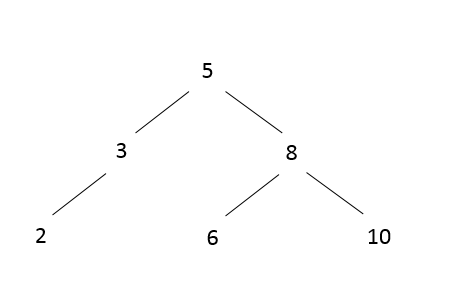
Based on the above property of BSTs, when a node is to be inserted into an existing BST, the location for the node can be uniquely determined. For example, if a node with key 6 needs to be inserted into the following BST

the BST will become

 

B. Implementation of the BST Data Structure

There are two approaches to BST implementation: array and linked list.

1. Array:

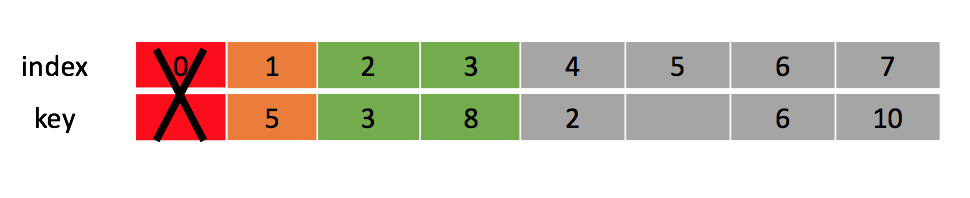
An approach to storing a BST is to use a single, contiguous block of memory cells, i.e., an array, for the entire tree. We store the tree’s root node in the first cell of the array. (Note that, for ease of implementation, we ignore the 0th cell and start from the 1st cell.) Then we store the left child of the root in the second cell, store the right child of the root in the third cell, and in general, continue to store the left and right children of the node found in cell n in the cells 2n and 2n+1, respectively. Using this technique, the tree below

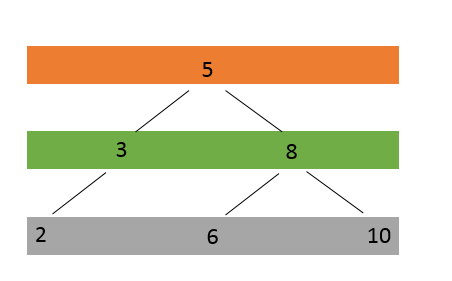
would be stored as follows

 

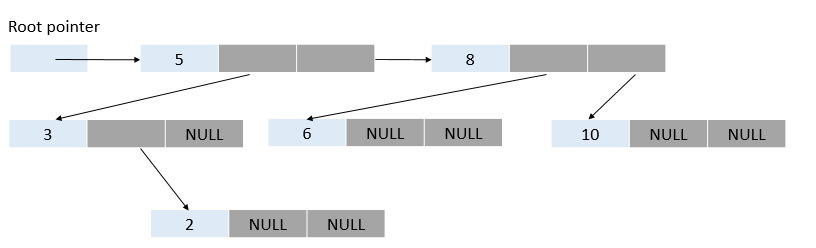
2. Linked list:

We set a special memory location, call a root pointer, where we store the address of the root node. Then each node in the tree must be set to point to the left or right child of the pertinent node or assigned the NULL value if there are no more nodes in that direction of the tree.

 

C. Detailed C++ Implementation for BST

Let’s see how the BST data structure can be realized in C++.We have two different approaches to BST implementation: array and linked list. Thus, we define four classes and use polymorphism as follows:

function.h

#ifndef function_h #define function_h #include <iostream> #include <math.h> using namespace std; class BST{ public: BST():Height(0){} virtual ~BST() {} virtual void insert(const int &) = 0; virtual bool search(const int &) const = 0; virtual void print() const = 0; int height() const { return Height; }// An empty tree has height of 0. A tree with only root node has height of 1. protected: int Height; }; class Array_BST : public BST{ public: Array_BST(); virtual ~Array_BST() {} virtual void insert(const int &) override; //root node is stored at index 1. virtual bool search(const int &) const override; virtual void print() const override{ int k = pow(2, height()); for (int i = 1; i <= k-1; i++) { if (array[i] != 0) cout << array[i] << " "; } } private: int array[1025]; }; class ListNode{ friend class List_BST; //make List_BST a friend public: ListNode(const int &info):key( info ),left( NULL ),right( NULL ) //constructor { }//end ListNode constructor private: int key; ListNode *left; ListNode *right; };//end class ListNode class List_BST : public BST{ public: List_BST(); virtual ~List_BST() { deleteTree(root); } virtual void insert(const int &) override; virtual bool search(const int &) const override; virtual void print() const override{ int i; for(i = 1; i <= Height; i++){ printGivenLevel(root, i); } } private: ListNode *root; // private member functions ListNode* createLeaf(int key) const; //new a ListNode and return its address /* clean a tree.*/ void deleteTree(ListNode *root); void printGivenLevel(ListNode* Ptr, int level) const { if (Ptr == NULL) return; if (level == 1) cout << Ptr->key << " "; else if (level > 1) { printGivenLevel(Ptr->left, level-1); printGivenLevel(Ptr->right, level-1); } } }; #endif /* function_h */

main.cpp

#include <iostream> #include <string.h> #include "function.h" using namespace std; void BSTManipulator(BST& bstobj1,BST& bstobj2, char cmd ){ int n; if (cmd == 'I') { cin >> n; bstobj1.insert(n); bstobj2.insert(n); }else if (cmd == 'S'){ cin >> n; if (bstobj1.search(n)) { cout << "yes" << endl; }else{ cout << "no" << endl; } if (bstobj2.search(n)) { cout << "yes" << endl; }else{ cout << "no" << endl; } }else if (cmd == 'H'){ cout << bstobj1.height() << endl;; cout << bstobj2.height() << endl;; }else if (cmd == 'P'){ bstobj1.print(); cout << endl; bstobj2.print(); cout << endl; } } int main(){ Array_BST A_bst; List_BST B_bst; char cmd; while (cin >> cmd) BSTManipulator(A_bst, B_bst, cmd); return 0; }

REQUIREMENTS:

Implement the constructor, insert(), search() member functions of both the Array_ BST and List_ BST classes and createLeaf(), deleteTree() of List_ BST class.

Note:

1. This problem involves three files.

• function.h: Class definitions.
• function.cpp: Member-function definitions.
• main.cpp: A driver program to test your class implementation.

You will be provided with main.cpp and function.h, and asked to implement function.cpp.

2.  For OJ submission:

     Step 1. Submit only your function.cpp into the submission block.

     Step 2. Check the results and debug your program if necessary.

Input

There are four kinds of commands:

• “I A”: insert a node with int value A into the BST
• “S A”: if the integer A exists in the BST, print “yes”; otherwise, print “no”.
• “P”: show the current content of the BST.
• “H”: print the BST’s height.

Each command is followed by a new line character.

Note: If a key is inserted before, it should be omitted.

Input terminated by EOF.

Output

The output shows the result of each command.

When the BST is empty, you don’t need to print anything except a new line character.

Sample Input  Download

Sample Output  Download

Partial Judge Code

11020.cpp

Partial Judge Header

11020.h

Tags

Discuss

Description

"Cat or Dog? that's a good question. " Shakespeare never said, 2019.

In this questions there are three types of animals class have to be implemented. (Cat , Dog and Caog)
Coag is a kind of special animal mixed in Cat and Dog.

Dog can only throwball
Cat can only play with carton.
Caog do those things both.

when Dog / Caog playing throwball output "it looks happy!\n"

when Cat  / Caog playing with carton output "it looks so happy!\n"

and also there's a zoo can count how many animals are in the zoo.

In this questions you have to implement 3 class (cat , dog and caog) based on the sample code.

Input

All input data would be finish in given main functions.

First number N would be N animals ( N < 10)

the following Ai numbers would types of animals.

And the T would be T instructions ( T < 30) 

the following Ti would be index and instructions

 

Output

 

When Animals born Zoo will auto output which kind of animal is born and how many animals in the zoo.

When Animals dead Zoo will auto output which kind of animal isdeadand how many animals in the zoo.

when Dog / Caog playing throwball output "it looks happy!\n"

when Cat  / Caog playing with carton output "it looks so happy!\n"

when Barking:

Cat would "meow!\n"

Dog would "woof!\n"

Caog would "woof!woof!meow!\n"

Sample Input  Download

Sample Output  Download

Partial Judge Code

12257.cpp

Partial Judge Header

12257.h

Tags

Discuss

Description

There is a function called "the one function",
the function is defined as:
F(N, M) = 1, if M <= N,
F(N, M) = F(N, M-1) + F(N, M - 2) + ... + F(N, M - N), if M > N

Given you N, M, tell the result of F(N, M) module 1000000009.

ouo.
Updated at: 2020/05/17 19:00, sorry for the typo in the description.

This is an exercise of operator overloading,
it is recommended that you can follow the partial judge code to finish your work.
There are 8 member functions and 1 additional function that you should implement.
Read the comments carefully to better understand the structure of the partial judge code.

You should choose 'c++11' as the option of submission.

For sample input 1,

N = 3, M = 5,
so F(3, 1) = F(3, 2) = F(3, 3) = 1,
and F(3, 4) =  F(3, 3) + F(3, 2) + F(3, 1) = 3
and F(3, 5) = F(3, 4) + F(3, 3) + F(3, 2) = 5
and F(3, 5) % 100000009 = 5,
so the output must be 5.

Input

The input contains 1 line,
the first line contains 2 numbers N, M.

It is guaranteed that:
1 <= N <= 100
1 <= M <= 10^9

Output

The output contains 1 line.

Output the answer of F(N, M), and a newline character at the end of line.

Sample Input  Download

Sample Output  Download

Partial Judge Code

12767.cpp

Partial Judge Header

12767.h

Tags

Discuss

Description

This is a partial judge problem Owo.
You're asked to implement several Codec that inherit the BaseCodec.

class BaseCodec {
public:
    virtual ~BaseCodec() {}
    virtual std::string encode(const std::string&) = 0;
};

There are three types of Codec.

The first one is the Reverse Codec, it should reverse the entire string.

The second one is the Compress Codec, it should replace the consecutive and repeated part with the count of the repeated part and a single instance of that character. Note that if the count is either 1 or 2, the length won't decrease after encoding, so you don't have to deal with the part that the count of the consecutive and repeated characters is either 1 or 2.

The third one is the Delay Codec, it should return the previous string that the user asked to encode. The first encoding request must return "None".

BaseCodec* getCodec(const std::string& name);

For the above function, you have to return the Codec Object according to the parameter name. The name of the Codec are "Reverse", "Compress" and "Delay", respectively.

For more information, you should refer to the main.cpp and function.h.

Input

The first line of the input contains a single integer N representing the number of Codec.
For the next N lines, each line contains a string, representing the type of the Codec from 0 to n - 1.
Next line contains a single integer Q representing the number of times of Encoding.
For the next Q lines, each line contains an integer representing the index of Codec and a string to do encoding on that Codec.

Constraint of testcases:

Testcase 1: Identical to the sample input.
Testcase 2 ~ 4: Contains only Reverse Codec.
Testcaes 5 ~ 7: Contains only Reverse Codec and Compress Codec.
Testcaes 8 ~ 10: Contains all three types of Codec.

Guarantee the string that use Reverse/Delay Codec contains only uppercase, lowercase alphabets and 0 ~ 9, and the string that use Compress Codec contains only uppercase and lowercase alphabets.

Output

For each time of Encoding, output the string after encoding. 

Sample Input  Download

Sample Output  Download

Partial Judge Code

13206.cpp

Partial Judge Header

13206.h

Tags

Discuss

Description

The task is to define the class ‘RleCodec’ for run-length encoding.

About implementing the virtual function:

We have the base class ‘Codec’ as an interface. The member functions in ‘Codec’ are pure virtual functions. Therefore we need to implement those virtual functions in the derived class ‘RleCodec’. The functions ‘decode’, ‘show’, ‘is_encoded’ are already done. The only function you need to complete is ‘RleCodec::encode’ in ‘function.cpp’.

In ‘main.cpp’, we see two functions having an argument of type ‘Codec&’:

    std::ostream& operator<<(std::ostream& os, Codec& data);

    void encode_decode(Codec& data);

Since ‘RleCodec’ is a derived class of ‘Codec’, we may pass an object of ‘RleCodec’ to the above two functions by reference as if it is an object of ‘Codec’. Calling ‘data.show(os);’ will invoke the virtual function of the corresponding derived class.

About run-length encoding:

The rule of run-length encoding is simple: Count the number of consecutive repeated characters in a string, and replace the repeated characters by the count and a single instance of the character. For example, if the input string is ‘AAADDDDDDDBBGGGGGCEEEE’, its run-length encoding will be ‘3A7DBB5GC4E’, because there are three A’s, seven D’s, … etc. Note that we do not need to encode runs of length one or two, since ‘2B’ and ‘1C’ are not shorter than ‘BB’ and ‘C’.

In ‘function.h’, we add the class ‘DummyCodec’ as a sample of implementing a derived class of the base class ‘Codec’. You do not need to change anything in ‘function.h’. The only function you need to write for this problem is the function ‘RleCodec::encode’ in ‘function.cpp’.

Hint: std::stringstream could be useful in solving this problem. Please refer to ‘RleCodec::decode’ for how to use std::stringstream.

You only need to submit ‘function.cpp’. OJ will compile it with ‘main.cpp’ and ‘function.h’.

We have already provided partial function.cpp belowed.

Note that if you can't use "auto".

For codeblock, go to the codeblock menu Settings --> Compiler ... --> Compiler flags and check Have g++ follow the C++11 ISO C++ language standard [-std=c++11]

For command line compiler, use g++ myprog.cpp -std=c++11 -o myprog

main.cpp

function.h

function.cpp

Input

A line contains several characters.

Output

There are four lines.

The first and second lines are dummy encoding and decoding. You don't need to implement it.

The third and fourth lines are RLE encoding and decoding.

Each line is followed by a new line character.

Sample Input  Download

Sample Output  Download

Partial Judge Code

13518.cpp

Partial Judge Header

13518.h

Tags

Discuss

Description

Array vs. Linked List

Array is a basic and fundamental concept in C/C++. It is a series of data which is arranged continiously in the memory space and can be accessed by index. Array is fast for indexing (using the given index to access the certain data), because the memory address of the destination can be calculated quickly. However, the capacity of the array is fixed after the declaration.

In I2PI (introduction of programming 1), we introduce a data structure called "linked list" which supports appending and deleting elements dynamically. The elements are stored in a series of "nodes", where each node points to the address of the next node. It is fast at appending elements but slow at indexing. To access the item of index i, you need to move i steps from head to obtain it.

Dynamic Array

In this problem, we will introduce a new data structure called "dynamic array" (abbreviated to "Darray" in the following statement) which supports dynamic capacity and indexing. We targeted to a simple Darray which has the following three variables

1. size : the number of elements stored in the array
2. capacity : the maximum number of elements which can be stored in the array
3. *data : the pointer which stores the address of the array

and two operations

1. pushback: append an element to the back
2. indexing : access the data by the given index.

To understand the concept of size and capacity, consider an array declaration:

 At first, the capacity is 5, but the size is 0 because no data is stored inside the array. Next, we push 5 elements to the array:

the capacity is still 5 but the size changes from 0 to 5. Therefore, no element can be appended to the array.

If we still want to append additional elements, we'll allocate a new array space with the double capacity and copy the data from old array to the new one. Note that the old array should be freed to avoid memory leak.

In this case, the capacity becomes 10 and the size is 6.

Implementation

You should implement the following functions based on the description above:

1. int& operator[](int): access data like using array. Users and main.cpp should/will not access the index which is greater or equal to size.
2. void pushback(int x): append the element x
3. void clear(void): clear the array (set size to 0) so that the next pushbacks will place elements in data[0],data[1] and so on.
4. int length(void): return the current size.
5. void resize(void): double the capacity and copy the data.
6. ~Darray(): destructor

Note that main.cpp acts like a functional tester for your Darray. There's no need to understand it. You should test your Darray by yourself.

More Notes: Time Complexity of Dynamic Array

Although it seems that copying the whole array will make dynamic array slow, we will analyze the time complexity to show that dynamic array is fast. Recall what Big-O Notation is where we introduced it in "The Josephus problem". O(2n+100)=O(2n)=O(n) means that the operation takes about n steps while O(2)=O(1) takes "constant" time. For array operations, we wish to have O(1) of indexing and pushback. In the following analysis, we will evaluate the amortized time complexity, which can be comprehended as calculating the average time complexity instead of the complexity of total operations.  Amortized time complexity = (complexity of total operations) / (number of operations).

Suppose that C₀ is the initial capacity and n is the number of operation of pushback. We discuss the time complexity in several cases:

1. Expand 0 time, n <= C₀.
   Since there's no expand operation, the total time complexity is O(1)*n=O(n). The amortized time complexity is O(n)/n=O(1).
2. Expand 1 time, C₀ < n <= C₁, C₁ = 2*C₀.
   Push C₀ items to array: O(C₀)
   Expand and copy: O(C₀), since there're C₀ elements to be copied.
   Push n-C₀ items to array: O(n-C₀)
   The total time complexity is O(C₀)+O(C₀)+O(n-C₀) = O(n+C₀). Since C₀ < n <= C₁, O(2C₀) < total time complexity <= O(3C₀). The amortized time complexity ranges in [O(3/2), O(2)). We identify it by the upper bound : O(2).
3. Expand 2 times, C1 < n <= C2, C2 = 2*C1.
   The amortized time complexity should be O(3). You can verify it by your own.

From the above analysis, if it expand i times, the amortized time complexity for appending an element is O(i+1). However, i won't be very large because the capacity grows exponentially so that we often regard the complexity as O(1), or, constant time. For instance, C₀=100, after expanding 20 times, the capacity will be 100*2²⁰≈10⁸.

---

 

Input

This is handled by the main function.

Output

This is handled by the main function.

Sample Input  Download

Sample Output  Download

Partial Judge Code

13520.cpp

Partial Judge Header

13520.h

Tags

Discuss