| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11891 | Postfix to Syntax Tree |
|
| 12725 | Minimum Spinning Tree |
|
| 13149 | Ternary Expression Evaluation |
|
| 13156 | Guess Left or Right |
|
| 13461 | Inorder 2 BTs |
|
Description
The input is a postfix Boolean expression, which has at most four variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. The task is to use this postfix expression to construct a syntax tree, and print the corresponding infix expression. For example, if the input is
AB|CD&&A|
then its syntax tree should be
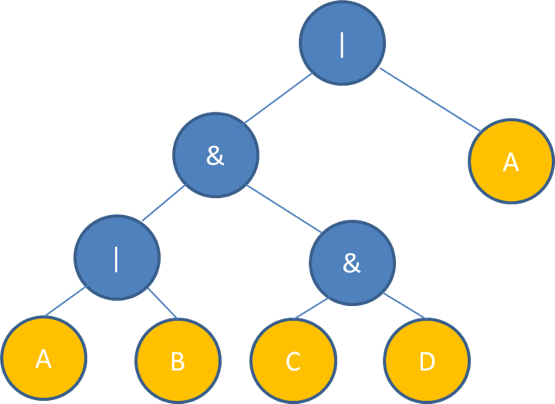
The corresponding infix expression with parenthesis is
A|B&(C&D)|A
You need to implement the function "constructTree()" based on the two files "main.c" and "function.h" given below.
For OJ submission:
You only need to copy and paste the code of your "function.c" into the submission block. Make sure you choose C compiler.
HINT :
Please read partial judge code first. We help you dealing with input :)
Input
The first line is a number N indicating the number of test cases. The next N lines contain the prefix Boolean expressions.
Output
The output contains N lines of the infix expressions with necessary parentheses.
Sample Input Download
Sample Output Download
Partial Judge Code
11891.cPartial Judge Header
11891.hTags
Discuss
Description
Disclaimer : This problem has nothing to do with MST(Minimum Spanning Tree). You don't need solid algorithm basic to solve this problem.
After doing a bunch of dull tree problems, you become dizzy and the trees look like they are spinning in your view.

You see an expression tree. The tree in your view can spin in two directions:
-
Left Spin: For a tree rooted at node P, of which right child is node Q and the left child of Q is B, after a left spin, the new root becomes Q, the left child of Q becomes P, and the right child of P becomes B. If P doesn't have a right child (i.e. Q is null), left spin cannot be performed. -
Right Spin: For a tree rooted at node Q, of which left child is node P and the right child of P is B, after a right spin, the new root becomes P, the right child of P becomes Q, the left child of Q becomes B. If Q doesn't have a left child (i.e. P null), right spin cannot be performed.
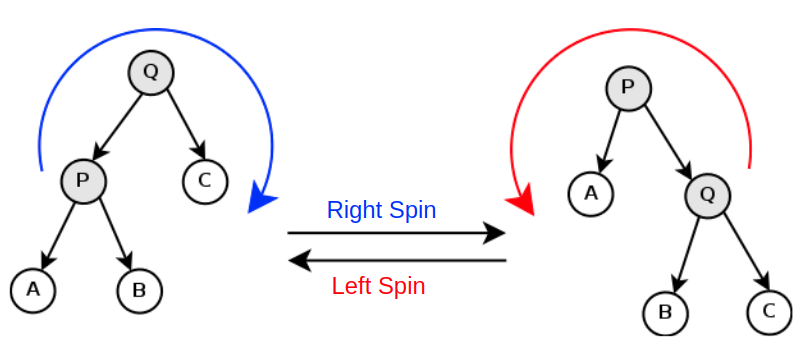
After several (or zero) times of spinning, if the expression tree can still denote a valid expression, we say that the tree is a good spinning tree; otherwise we say that the tree is a bad spinning tree.
The evaluation of the tree changes after the tree spins. Given an evaluation tree, you want to know that what is the minimum evaluation among all good spinning trees.
Explanation of Sample IO
For the given expression tree, it has four good spinning trees which are shown in the below figure. Initially its evaluation is -8. After one left spin, its evaluation becomes 0. After two left spins, its evaluation becomes -6. After one right spin, its evaluation becomes 0. It is obvious that after three left spins or two right spins, the tree cannot donate a valid expression. Therefore the minimum spinning tree is the inital tree and therefore output -8.
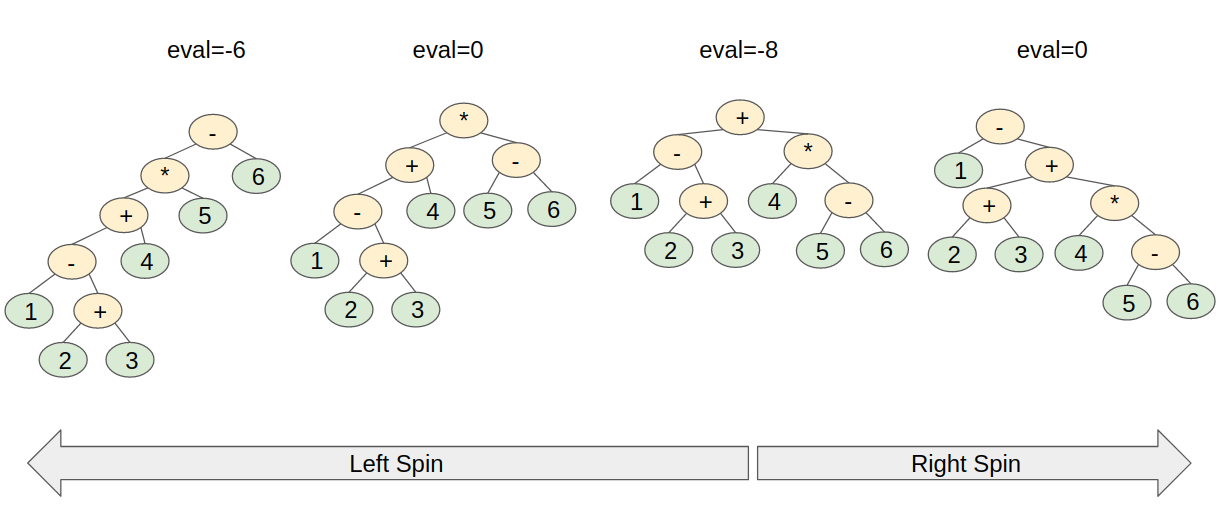
Input
The first line of the input is an integer N(3 <= N <= 3x105), being the length of the prefix expression of the expression tree.
The next line is the expression tree (in prefix expression). The expression contains only +, -, * and digits. All the numbers in the expression are integers between 1 and 9.
Test Cases
-
For all test cases, it is guaranteed values during calculation is between [-109, 109], meaning that using 32-bit integer will not overflow (if your code does not have bugs).
-
1-st test case : same as sample IO
-
2-nd test case : N <= 50. It is guaranteed that there are only three good spinning trees : the giving tree, the tree that left spins once, and the tree that right spin once. (i.e. evaluate the three good spinning trees and output the minimum value, and then you get AC in this test case)
-
3-rd, 4-th test case : You can get AC using an O(N2) solution.
-
5-th test case : You need to come up with an O(N) solution to get an AC.
Output
Output the minimum evaluation among all good spinning trees.
Note that you should have a '\n' in the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The ternary operator is an operator in C. Its syntax is as follows:
It is often used to replace a simple if-else statement such as:
You can also combine several ternary operators together such as:
Now you are given a ternary expression, in which all the values are either true or false. Next you must evaluate the ternary expression with different combinations of values.
More specifically, a valid ternary expression is either:
or
And the evaluation order of a ternary expression can be explained as follows:
- If the valid ternary expression is a single value, then just return the value.
- Otherwise:
- if the value before ? is true then replace this ternary expression as the value of the ternary expression between ? and :
- if the value before ? is false then replace this ternary expression as the value of the ternary expression after :
Hint: You can apply the idea of a syntax tree to solve this problem.
Input
The first line of the input is a valid ternary expression that contains the ternary operators and value indices.
- It is guaranteed that the value indices are pairwise distinct and range from 1 to the number of values in this ternary expression.
- For example, in the sample input below, the number of values is 5, and the value indices from left to right is 5, 3, 2, 4, 1, respectively.
The next line contains a single integer T, (T <= 5000), representing the number of combinations you have to evaluate.
For the next T lines, each line contains a binary string whose length is equal to the number of values in the ternary expression, giving the setting of each value.
- Note that the i-th character in this binary string (counted from left) is for the value index i. (1 represents true and 0 represents false)
- For string "01101", value indices 1-5 are set as 0,1,1,0,1, respectively.
There are 5 testcases in this problem.
For the first 3 testcases: 1 <= number of values <= 5
For the rest of the testcases: 1 <= number of values <= 3001
Output
For each combination, output the value of the ternary expression. (1 represents true and 0 represents false)
Remember to add a newline character at the end of every line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Today is your birthday, your father wants to prepare a gift for you. He ranks his brains and finally decide what to give. Since you are a college student major in computer science, he gives you a rooted binary tree for your birthday! But at the time you are unpacking the gift, you accidentally damage the binary tree! What a pity! You have tried very hard to restore the information of the binary tree but end up failure. For each node, you know which two nodes are its children, but you don't know which one is left child and which one is right child.
Fortunately, There's an inorder traversal sequence of the binary tree on the package, and you want to know whether the broken information of the binary tree is possible to form the inorder traversal sequence on the package.
Note:
The following figure is the way to form the tree that meets the input of sample testcase 1 and its inorder traversal is identical to the input inorder traversal.
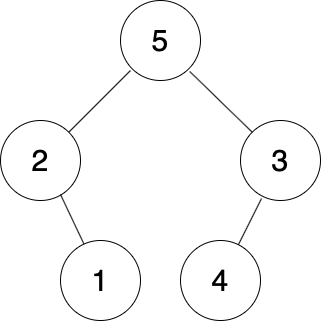
Input
The input contains T testcases.
The first line of each testcase contains a single integer N representing the number of node in the binary tree. The index of nodes in the binary tree is 1-based.
For the following N lines, each line contains two integers. For i-th line, the two integers represent the children of i-th node. 0 represents that the node doesn't exist.
Next line of the input contains N integers representing the inorder traversal sequence.
Constraint of testcases:
Testcase 1: N <= 5, T <= 4.
Testcase 2: T = 20, N <= 15, and node 1 is guarantee to be the root of the binary tree.
Testcase 3: T = 20, N <= 2000, and node 1 is guarantee to be the root of the binary tree.
Testcase 4: N * T <= 4 * 106, N <= 2 * 105, and node 1 is guarantee to be the root of the binary tree.
Testcase 5: T = 20, N <= 15.
Testcase 6: T = 20, N <= 2000.
Testcaes 7: T = 20000, N <= 10.
Testcase 8 ~ 10: N * T <= 4 * 106, N <= 2 * 105.
Output
For each testcase, if there exists a way to distribute nodes to left child or right child that its inorder traversal is identical to the input inorder traversal, then output "YES" otherwise "NO".
Remember to add a newline character at the end of every line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are given an Inorder Traversal sequence.
Find all possible Binary Trees with the given Inorder traversal and print their preorder traversals.
Below are all possible different binary trees with the same inorder {1, 2, 3}:
1 1 2 3 3 \ \ / \ / / 2 3 1 3 1 2 \ / \ / 3 2 2 1
Input
Only an integer N, 1 <= N <= 10, giving that the inorder traversal sequence is {1, 2, 3, ..., N}.
Output
Output all the possible preorder traversals in lexicographical order.
Remember to add a new line in the end.