| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 10966 | Infix to syntax tree |
|
| 10968 | Prefix to infix |
|
| 10972 | Remove unnecessary parentheses |
|
| 11847 | Prefix Boolean expression |
|
| 13140 | Wubalubadubdub |
|
| 13452 | Walk on the tree |
|
Description
Given an infix Boolean expression with parentheses, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. Build a corresponding syntax tree for it.
To parse the infix expression with parentheses, use the grammar below.
EXPR = FACTOR | EXPR OP FACTOR
FACTOR = ID | (EXPR)
EXPR is the expression, ID is one of ‘A’, ‘B’, ’C’, or ‘D’, and OP is one of ‘&’ or ‘|’.
You will be provided with main.c and function.h. main.c contains the implementation of functions printPrefix and freeTree. function.h contains the definition of tree node and variables. You only need to implement the following three functions in function.c.
BTNode* makeNode(char c) // create a node without any child
BTNode* EXPR() // parse an infix expression and generate a syntax tree
BTNode* FACTOR() // use the parse grammar FACTOR = ID | (EXPR) to deal with parentheses
For OJ submission:
Step 1. Submit only your function.c into the submission block.(Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
The input contains N infix expressions, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, two operators ‘&’ and ‘|’, and parentheses. All parentheses are matched.
Output
The output contains N prefix expressions without parentheses, which are preorders of syntax trees.
Sample Input Download
Sample Output Download
Partial Judge Code
10966.cPartial Judge Header
10966.hTags
Discuss
Description
Given an prefix Boolean expression, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. Output its infix presentation with necessary parenthesis.
- Ex: input: ||A&BCD
output: A|(B&C)|D
Hint : About necessary parenthesis, you can observe the syntax tree which has been constructed, then you will find out the rule. For example, the infix expression of |&|AB&CDA with necessary parenthesis is A|B&(C&D)|A, rather than (A|B)&(C&D)|A .
- Syntax tree of |&|AB&CDA
You will be provided with main.c and function.h, and asked to implement function.c.
For OJ submission:
Step 1. Submit only your function.c into the submission block.(Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
The first line will have a number N with the number of test cases, followed by N lines of input, each contain the prefix Boolean expression.
Output
There are N lines infix expression with necessary parenthesis.
Sample Input Download
Sample Output Download
Partial Judge Code
10968.cPartial Judge Header
10968.hTags
Discuss
Description
Given an infix Boolean expression with parentheses, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. Please remove unnecessary parentheses and print the infix expression. Existence of unnecessary parentheses doesn’t affect the result of expression. For example,
(A&B)|(C&D) → A&B|(C&D)
(((A|B))) → A|B
Hint: You can combine two homework. Build a syntax tree and print the infix expression with necessary parentheses.
For OJ submission:
Step 1. Submit your main.c into the submission block.(Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
The input is an infix expression, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, two operators ‘&’ and ‘|’, and parentheses. The length of the infix expression is less than 256.
Output
The output is an infix expression without unnecessary parentheses.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Give a prefix Boolean expression, which only has at most 4 variables ‘A’, ‘B’, ‘C’, and ‘D’, and 2 operators, AND ‘&’ and OR ‘|’, print its truth table.
For example, if input is "|&AC|AB", then result will be
A B C D output
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 1
0 1 0 1 1
0 1 1 0 1
0 1 1 1 1
1 0 0 0 1
1 0 0 1 1
1 0 1 0 1
1 0 1 1 1
1 1 0 0 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
Input
The input contains a sequences of prefix expression. It only has at most 4 variables ‘A’, ‘B’, ‘C’, and ‘D’, and 2 operators, AND ‘&’ and OR ‘|’. The length of prefix expression is shorter than 30.
Output
It has 5 variables 'A', 'B', 'C', 'D', and output, each variable is separated by a space.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
A binary search tree is a binary tree that has the following properties:
-
For any node, its key is greater than the keys stored in the left subtree.
-
For any node, its key is smaller than the keys stored in the right subtree.
-
For any node, the left subtree and the right subtree are binary search trees respectively as well.
-
Every node has a unique key. No two nodes share the same key.
Reference: Build a Binary Search Tree from a postorder sequence
For example, the two following trees are binary search trees.
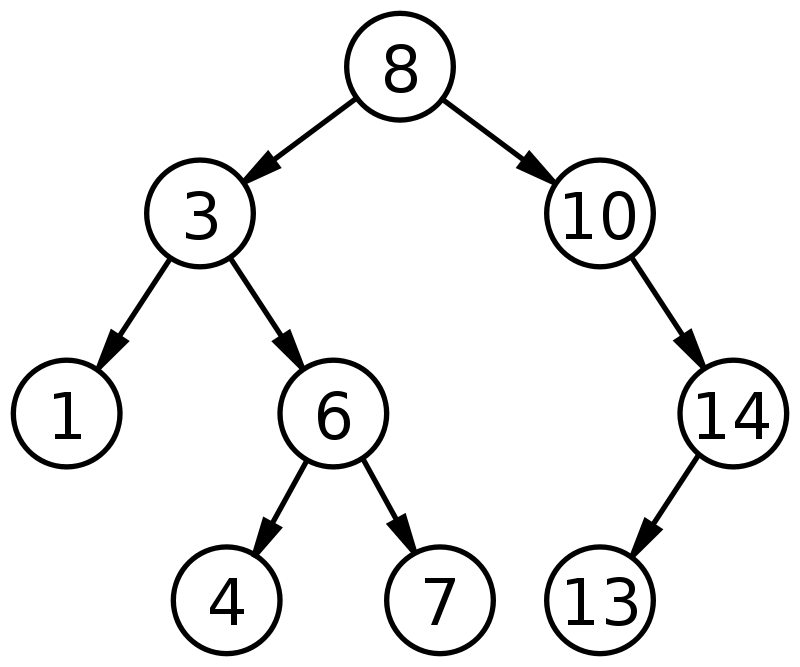
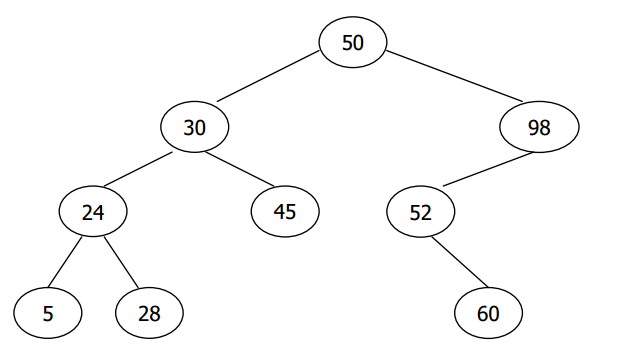
Now, given a postorder of a binary search tree, please output the preorder of it.
The graph of the sample input is as follow.
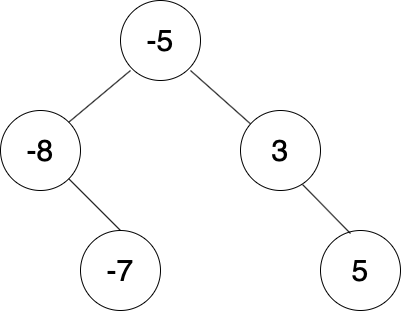
Input
The input contains only one line represent the postorder of the binary tree. The value are pairwise distinct.
a1 a2 a3 ...... aN
(1 <= N <= 200000, -1000000000 <= a_i <= 1000000000)
Output
Please output the preorder of the binary search tree according to the input.
Guarantee that there's only one answer since we can prove that no two different binary tree have the same postorder and inorder.
Remember to output newline character at the end of the line.
Don't output additional space at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are given a binary tree of N vertices numbered from 1 to N.
There are Q qustions.
Print the every direction if you want to walk from node A to node B.
P: move to parent
R: move to right child
L: move to left child
Input
The first line contains a single integer N (2≤N≤3000).
Next N lines contain 2 integers, represent the left child and the right child of the i th node. (and 0 means empty)
Next line contains a integer Q (1≤Q≤3000);
The next Q lines contain two integers, A, B.
Output
For each question, output every direction that walks from node A to node B.
Remember add a new line in the end of each question.