| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13129 | Prize! |
|
| 13436 | Remove the leaves |
|
Description
There are n people in a circle, numbered from 1 to n in clockwise direction. They are playing a game, and there will be m lucky people that can get the prizes.
Rules of the game:
1. Each prize has a lucky number.
2. Who is counted as the lucky number can get a prize.
3. If the lucky number is odd, count clockwise.
4. If the lucky number is even, count counterclockwise.
5. The student who gets a prize shall leave the circle.
6. After someone left the circle, if the new lucky number is odd, count from the next person, otherwise count from the previous person (in clockwise order).
For example:
n = 8
m = 3
lucky number = 3 4 5
The sequence of getting prize is:
first number is 3, so count clockwise starting from 1: 1 2 3
second is 4, so we count from 2, and counterclockwise: 2 1 8 7
last number is 5, so we count from 8, and clockwise: 8 1 2 4 5
Then people 3, 7, 5 can get the prize.
Please use doubly circular linked list to solve this problem.
Input
The first line has two integer n and m, where n is the number of total people, and m is the number of prizes.
The second line has m positive number a1 ~ am.
testcases:
1. 1 <= m <= n <= 10000, 1 <= ai <= n
2. 1 <= m <= n <= 10000, 1 <= ai <= n
3. 1 <= m <= n <= 10000, 1 <= ai <= n
4. 1 <= m <= n <= 1000000, 1 <= ai <= 10000000, n*m <= 300000000
5. 1 <= k <= n <= 1000000, 1 <= ai <= 10000000, n*m <= 300000000
6. 1 <= k <= n <= 1000000, 1 <= ai <= 10000000, n*m <= 300000000
Output
The output has m lines, each line contains a number: who can get the prize.
Sample Input Download
Sample Output Download
Partial Judge Code
13129.cPartial Judge Header
13129.hTags
Discuss
Description
Mr. Kuo is an adventurer. One day, he finds a special "tree".
The tree consists of N vertices.
There are exactly one simple path between any two vertices.
Mr. Kuo wants to do the following operation K times to this tree:
- If the tree is empty, do nothing.
- If the tree consists of one vertex, remove this vertex.
- If the tree consists of two vertices, remove both vertices.
- Otherwise, remove all the leaf of the tree.
(A leaf of a tree is a vertex that is connected to at most one vertex.)
Mr. Kuo is wondering how many vertices will remain after he performs the operations K times.
Take the sample test as the example:
- In test case 1, {2, 4, 5, 7, 9, 12, 13} are removed and {1, 3, 6, 8, 10, 11} remain.
- In test case 2, {1, 2} are removed and no vertex remains.
- In test case 3, {1, 2, 6, 7} are removed and {3, 4, 5} remain.
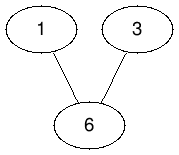
- In test case 4, {2, 4, 5} are removed and {1, 3, 6} remain.
- In test case 5, no vertices are removed and {1, 2, 3} remain.
The picture below is the tree of the test case 4 in the sample test.
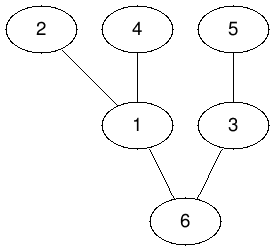
The picture below is the tree after Mr. Kuo performs the operation once.
Input
The first line contains one integer T — the number of test cases. Description of the test cases follows.
The first line of each test cases contains two integer N K — the number of vertices in the tree and the number of operations Mr. Kuo performs.
Each of the next N - 1 lines contains two integers ui and vi — there is an edge between ui and vi.
For each test:
- T ≤ 100, N ≤ 20
- T ≤ 100, N ≤ 100
- T ≤ 100, N ≤ 500
- T ≤ 100, N ≤ 1000
- T ≤ 100, N ≤ 5000
- T ≤ 100, N ≤ 20000
1 ≤ ui, vi ≤ N
0 ≤ K ≤ N for all test.
Output
For each test case print an integer — the number of verticees remain in the tree.