Description

This problem will give you a sequence of positive integers.  Use this sequence to create a linked list to store those integers.  Next, the problem will give you another sequence of positive integers, p₀, p₁,…p_k-1.  Delete the nodes in the position at p₀, p₁, …p_k-1 of the linked list, where 1<=p₀<p₁<…p_k-1<=N. If the node is not existing,do nothing. And show the final results.

For example, if the first sequence is 1, 2, 3, 4, 5, 6,7, a linked list is created as

If the second sequence is 1, 1, 4, do the follows.

After p₁=1, the list becomes

because the first node is 1.  After p₂ = 1, the list becomes

because the first node is 2.  After p₃ = 4, the list becomes

because the fourth node is 6.

 

The framework of the program is provided.

1. Create a linked list from the input  (createList)
2. while there are still some data pi
3.     read in pi 
4.     delete node at pi  (deleteNode)
5. print the remaining list (printList)
6. free the list (freeList)

You will be provided with main.c and function.h. main.c contains the implementation of function printList, and freeList, and function.h contains the definition of node and the interface of createList(&head) and deleteNode(&head, pi).  You only need to implement createList(&head) and deleteNode(&head, pi) in function.c, in which head is the head of the linked list, and pi is the node at pi to be deleted.

 

You will be provided with main.c and function.h, and asked to implement function.c.

For OJ submission:

       Step 1. Submit only your function.c into the submission block. (Please choose c compiler) 

       Step 2. Check the results and debug your program if necessary.

main.c

#include <stdio.h> #include <stdlib.h> #include "function.h" void printList(Node *head){ Node *temp; for(temp = head; temp!=NULL; temp=temp->next) { printf("%d ", temp->data); } } void freeList(Node *head){ Node *temp; for(temp=head; temp!=NULL; temp=head){ head = head->next; free(temp); } } int main() { Node *head; int data; head = createList(); while(1){ scanf("%d", &data); if(data>-1){ deleteNode(&head,data); }else break; } printList(head); freeList(head); return 0; }

function.h

#include <stdlib.h> #include <stdio.h> typedef struct _Node { int data; struct _Node *next; } Node; void deleteNode(Node ** nd, int data); Node* createList();

Input

The input contains 2 sequence of positive integers as the linklist and the order, except the last one, which is -1, indicating the end of the sequence. 

Output

The output contains the sequence of resulting linklist.

Sample Input  Download

Sample Output  Download

Partial Judge Code

10947.c

Partial Judge Header

10947.h

Tags

Discuss

Description

Define the level 1 string s1 = “OuQ”,
and the level k string sk = “O” + sk−1 + “u” + sk−1 + “Q”.

For example:

• s2 = “O” + s1 + “u” + s1 + “Q” = “OOuQuOuQQ”
• s3 = “OOOuQuOuQQuOOuQuOuQQQ”

Given 3 integeres k,l,r.
Please find all characters of sk[l],sk[l+1],...sk[r−1],sk[r]

Input

There’re multiple testcases in input.
Three integers k,l,r on each line.

• 1 ≤ k ≤ 50
• 0 ≤ l ≤ r < length of sk
• 1 ≤ |r−l+1| ≤ 100

Output

For each testcase, print |r−l+1| characters,sk[l],sk[l+1],...sk[r−1],sk[r], for a line.

Remember ‘\n’ on the end of each line.

Sample Input  Download

Sample Output  Download

Tags

Discuss

Description

N queens problem asks how many ways to place N non-attacking queens on an N×N chessboard.

For example, there’re 2 solutions for N = 4:
( 0 means empty spot, Q means queen. )

0 Q 0 0     0 0 Q 0
0 0 0 Q     Q 0 0 0
Q 0 0 0     0 0 0 Q
0 0 Q 0     0 Q 0 0

While, there’s no solution for N = 2:
Below is the all placements. All of them contains queens threaten each other.

Q Q    Q 0    Q 0    0 Q    0 Q    0 0
0 0    Q 0    0 Q    Q 0    0 Q    Q Q

Let’s define a new problem “N-Queens M-Rooks Problem”.
It asks how many ways to place N queens and M rooks on an (N+M)×(N+M)( chessboard such that no two of queens or rooks can attack each other in 1 step.

For N = 1, M = 2, there’re 4 solutions:
( 0 means empty spot, Q means queen, R means rook. )

Q 0 0    0 R 0
0 0 R    R 0 0
0 R 0    0 0 Q

0 R 0    0 0 Q
0 0 R    R 0 0
Q 0 0    0 R 0

Possible move of Queen:

Possible move of Rook:

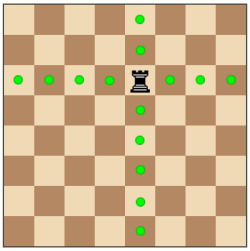
Input

There’re multiple testcases.
Each testcase is consisted of 2 integers N,M on one line.

It’s guaranteed that:

• 0 ≤ N, M ≤ 9
• 1 ≤ N+M ≤ 9

Output

Print the number of solution for N-Queens M-Rooks Problem for every testcase.
Remember ‘\n’ on the end of line.

Sample Input  Download

Sample Output  Download

Tags

Discuss