| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13129 | Prize! |
|
| 13137 | binary search tree |
|
| 13431 | Palindrome Linked List |
|
| 13435 | Longest path on a tree |
|
Description
There are n people in a circle, numbered from 1 to n in clockwise direction. They are playing a game, and there will be m lucky people that can get the prizes.
Rules of the game:
1. Each prize has a lucky number.
2. Who is counted as the lucky number can get a prize.
3. If the lucky number is odd, count clockwise.
4. If the lucky number is even, count counterclockwise.
5. The student who gets a prize shall leave the circle.
6. After someone left the circle, if the new lucky number is odd, count from the next person, otherwise count from the previous person (in clockwise order).
For example:
n = 8
m = 3
lucky number = 3 4 5
The sequence of getting prize is:
first number is 3, so count clockwise starting from 1: 1 2 3
second is 4, so we count from 2, and counterclockwise: 2 1 8 7
last number is 5, so we count from 8, and clockwise: 8 1 2 4 5
Then people 3, 7, 5 can get the prize.
Please use doubly circular linked list to solve this problem.
Input
The first line has two integer n and m, where n is the number of total people, and m is the number of prizes.
The second line has m positive number a1 ~ am.
testcases:
1. 1 <= m <= n <= 10000, 1 <= ai <= n
2. 1 <= m <= n <= 10000, 1 <= ai <= n
3. 1 <= m <= n <= 10000, 1 <= ai <= n
4. 1 <= m <= n <= 1000000, 1 <= ai <= 10000000, n*m <= 300000000
5. 1 <= k <= n <= 1000000, 1 <= ai <= 10000000, n*m <= 300000000
6. 1 <= k <= n <= 1000000, 1 <= ai <= 10000000, n*m <= 300000000
Output
The output has m lines, each line contains a number: who can get the prize.
Sample Input Download
Sample Output Download
Partial Judge Code
13129.cPartial Judge Header
13129.hTags
Discuss
Description
There's an empty binary search tree, you have to implement two functions:
1. add_node:
- If the tree is empty, the node will be the root node of this tree.
- Otherwise, start to compare with the root node, if the new node is smaller than it, compare with the leftchild, otherwise, compare with the rightchild, until there is no node to compare, place the new node.
- For example:
- There is a binary search tree
- add 7 to this tree
- compare with the root
- 7 >= 5, compare with the rightchild
- 7 < 10, compare with the leftchild
- 7 <= 8 and node 8 has no leftchild, so put 7 to the leftchild of node 8, the tree will be like:
2. showtree: output this tree in in-order
Input
The first line contains a integer n, means how many node to add.
The second line contains n number a1 ~ an, means the value of n node.
testcases:
1. n <= 1000, 0 <= ai <= 109, the sequence of n numbers is increasing.
2. n <= 1000, 0 <= ai <= 109, the sequence of n number is decreasing.
3. n <= 1000, 0 <= ai <= 109.
Output
The output has only one line, contains n numbers, the in-order traversal of binary search tree.
please output a whitespace after every number.
Sample Input Download
Sample Output Download
Partial Judge Code
13137.cPartial Judge Header
13137.hTags
Discuss
Description
Do you notice that the ID of this problem is a palindrome number? This problem, though, requires you to determine whether a linked list is a palindrome - it reads the same backwards as forwards.
Please implement a function to detect whether the linked list given is a palindrome or not.
Input
Since this problem is judged partially, you needn't be concerned about the format of input.
The length of the linked list is at least 1 and won't exceed 100000.
In case your're interested in sample I/O, there are several test cases in a file, which starts with a interger n indicating the length of the list and the next line contains n intergers.
Output
Since this problem is judged partially, you needn't be concerned about the format of output.
In case your're interested in sample I/O, for each test case, if the list is a palindrome, it should print a single T, otherwise print a F. There should be a new line at the end of file (EOF).
Sample Input Download
Sample Output Download
Partial Judge Code
13431.cPartial Judge Header
13431.hTags
Discuss
Description
Mr. Kuo is an adventurer. One day, he finds a maze.
The maze has N rooms. There may be a tunnel between rooms.
There is exactly one simple path between any two different rooms. That is, the maze is a "tree".
Mr. Kuo is curious about the length of the longest path in this maze.
Take the sample test as the example:
- The longest path of the 1st test case is (2 → 1 → 3), whose length is 2.
- The longest path of the 2nd test case is (1 → 2 → 3), whose length is 2.
- The longest path of the 3rd test case is (5 → 7 → 3 → 1 → 4 → 2), whose length is 5.
[Hint]
Instead of performing DFS twice, there is a solution to find the diameter in one DFS. For any tree whose root is \(i\), if we have two properties of its subtrees / children (\(j\)): the longest distance of the (sub-)tree (denoted by \(d\)) and the longest distance to any leaf (denoted by \(p\)). Then we have \(p_i=\displaystyle\max_{\forall j\text{ is a child of }i}(p_j+1)\), and \(d_i\) is either in its subtrees: \(\displaystyle\max_{\forall j\text{ is a child of }i}d_j\) or passing through the root: \(p_i+\displaystyle\max_{\forall j'\text{ is a child of }i}(p_{j'}+1)\), where \(j'\) mustn't be the same as we took in \(p_i\).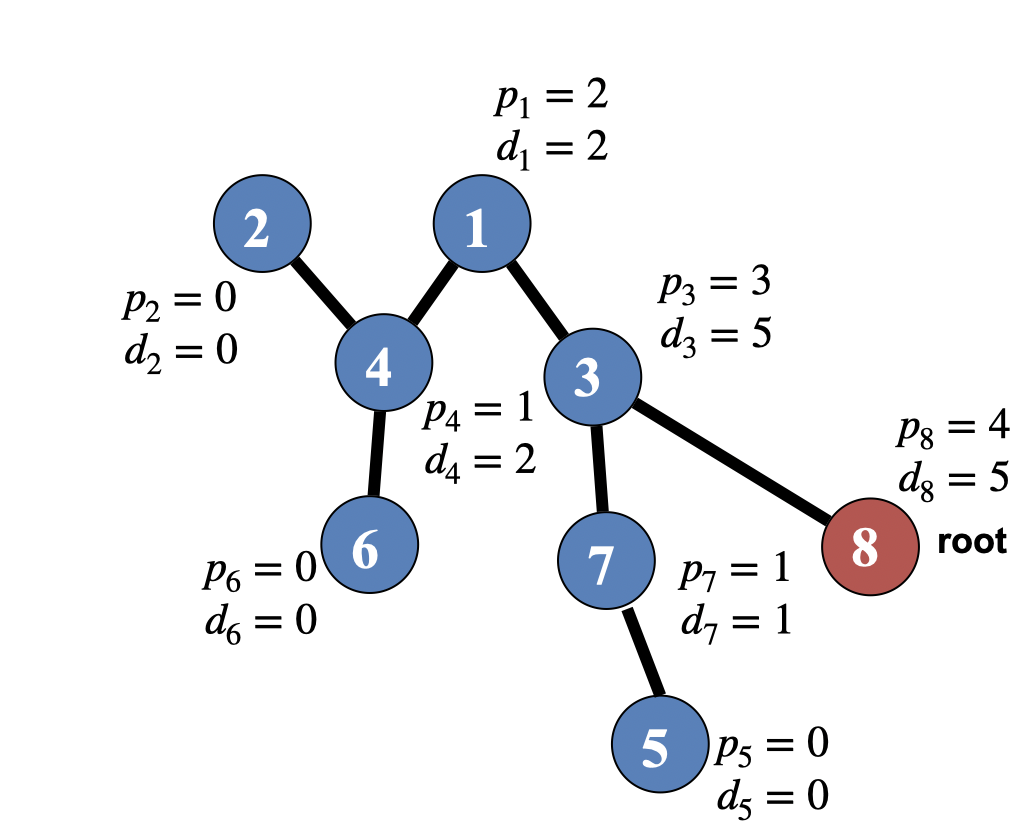
Input
The first line contains one integer T — the number of test cases. Description of the test cases follows.
The first line of each test case contains an integer N — the number of rooms in the maze.
Each of the next N - 1 line contains two integers ui and vi — there is a tunnel between ui and vi.
For each test:
- T ≤ 10, N ≤ 10
- T ≤ 10, N ≤ 100
- T ≤ 10, N ≤ 500
- T ≤ 10, N ≤ 1000
- T ≤ 10, N ≤ 10000
- T ≤ 30, N ≤ 20000
Output
For each test case print an integer — the length of the longest path in the maze.