| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12602 | OuQ String |
|
| 12604 | N-Queens M-Rooks Problem |
|
Description
Define the level 1 string s1 = “OuQ”,
and the level k string sk = “O” + sk−1 + “u” + sk−1 + “Q”.
For example:
- s2 = “O” + s1 + “u” + s1 + “Q” = “OOuQuOuQQ”
- s3 = “OOOuQuOuQQuOOuQuOuQQQ”
Given 3 integeres k,l,r.
Please find all characters of sk[l],sk[l+1],...sk[r−1],sk[r]
Input
There’re multiple testcases in input.
Three integers k,l,r on each line.
- 1 ≤ k ≤ 50
- 0 ≤ l ≤ r < length of sk
- 1 ≤ |r−l+1| ≤ 100
Output
For each testcase, print |r−l+1| characters,sk[l],sk[l+1],...sk[r−1],sk[r], for a line.
Remember ‘\n’ on the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
N queens problem asks how many ways to place N non-attacking queens on an N×N chessboard.
For example, there’re 2 solutions for N = 4:
( 0 means empty spot, Q means queen. )
0 Q 0 0 0 0 Q 0
0 0 0 Q Q 0 0 0
Q 0 0 0 0 0 0 Q
0 0 Q 0 0 Q 0 0
While, there’s no solution for N = 2:
Below is the all placements. All of them contains queens threaten each other.
Q Q Q 0 Q 0 0 Q 0 Q 0 0
0 0 Q 0 0 Q Q 0 0 Q Q Q
Let’s define a new problem “N-Queens M-Rooks Problem”.
It asks how many ways to place N queens and M rooks on an (N+M)×(N+M)( chessboard such that no two of queens or rooks can attack each other in 1 step.
For N = 1, M = 2, there’re 4 solutions:
( 0 means empty spot, Q means queen, R means rook. )
Q 0 0 0 R 0
0 0 R R 0 0
0 R 0 0 0 Q
0 R 0 0 0 Q
0 0 R R 0 0
Q 0 0 0 R 0
Possible move of Queen:

Possible move of Rook:
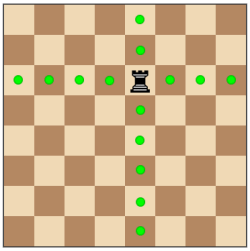
Input
There’re multiple testcases.
Each testcase is consisted of 2 integers N,M on one line.
It’s guaranteed that:
- 0 ≤ N, M ≤ 9
- 1 ≤ N+M ≤ 9
Output
Print the number of solution for N-Queens M-Rooks Problem for every testcase.
Remember ‘\n’ on the end of line.