| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13337 | Karpet Sierpinski |
|
| 13419 | I hate New Year |
|
| 13420 | Domo travels around the world |
|
Description
This can be solved with recursion.
The Sierpinski Carpet is a self-similar pattern with 8 non-overlapping copies of itself.
It starts with a white square divided into 9 smaller subsquares, which interior square is filled with black (Depth = 1).
To obtain a carpet at Depth = 2, do the same procedure recursively to the remaining 8 subsquares.
Here is an example of the carpet with Depth 1, 2, 3, & 4.

Input
Input contains single integer n, the Depth of the carpet (1 <= n <= 8).
Output
Please output the Sierpiński carpet of side length 3n and use '.' to represent white, '#' to represent black.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Although you think that Christmas is the last torture this year, you found that you have to send red envelope to all of your cousins because your mom "suggest" you.


Since the number of money is also a non-unique integer,you want to follow the rule in 13412 - I hate Christmas but with some modification.
First, you rearrange the order with the following rule:
Given the head of the linked list containing multiple groups (the size of each group is k ), reverse the nodes inside each group at a time.
k is a positive integer and is less than or equal to the length of the linked list.
If the number of nodes is not a multiple of k, then the left-out nodes in the end should remain the same order.
You are not allowed to alter the values in each node.
For example, when k = 2:

Next, different from the 13412 - I hate Christmas, you have to reverse the whole list so the kids who want to get the red envelope first will become the last :) .
For example,
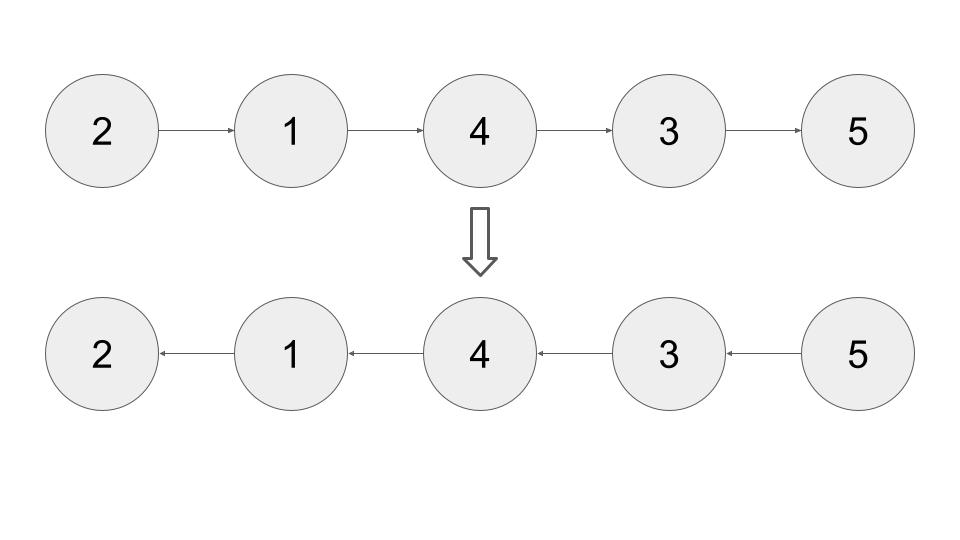
Note that it is a partial-judge problem that you need to implement the function:
Input
The first line is composed of a sequence of integer(1<= val <=100000000), which represents the values of the linked list.
The input stops when read in '-1' ('-1' is not a part of the 2 linked-lists).
The second line is k, the size of the group that will be reversed.(1 <= k <= length of the linked list)
Output
The values of the final reversed linked-list.
The values are separated by a whitespace and the output is also ended with a whitespace.
Sample Input Download
Sample Output Download
Partial Judge Code
13419.cPartial Judge Header
13419.hTags
Discuss
Description

(Domo's friend Kao who gives him the VIP service)
Domo is a brilliant dog, but after this semester, he is very tired and needs to have some rest. Hence, he wants to travel around the world.
Luckily, Domo's friend gives him the VIP service, which can have a flight for free between some cities.
Now, given the number of cities and the free flight list, and Domo starts its travel from the city 0, please find out that how many tickets Domo needs to buy to travel to all the cities (you need 1 ticket to travel from one city to another).
For example, the sample gives 6 cities and 4 pairs of free flights (black line) shown as below:
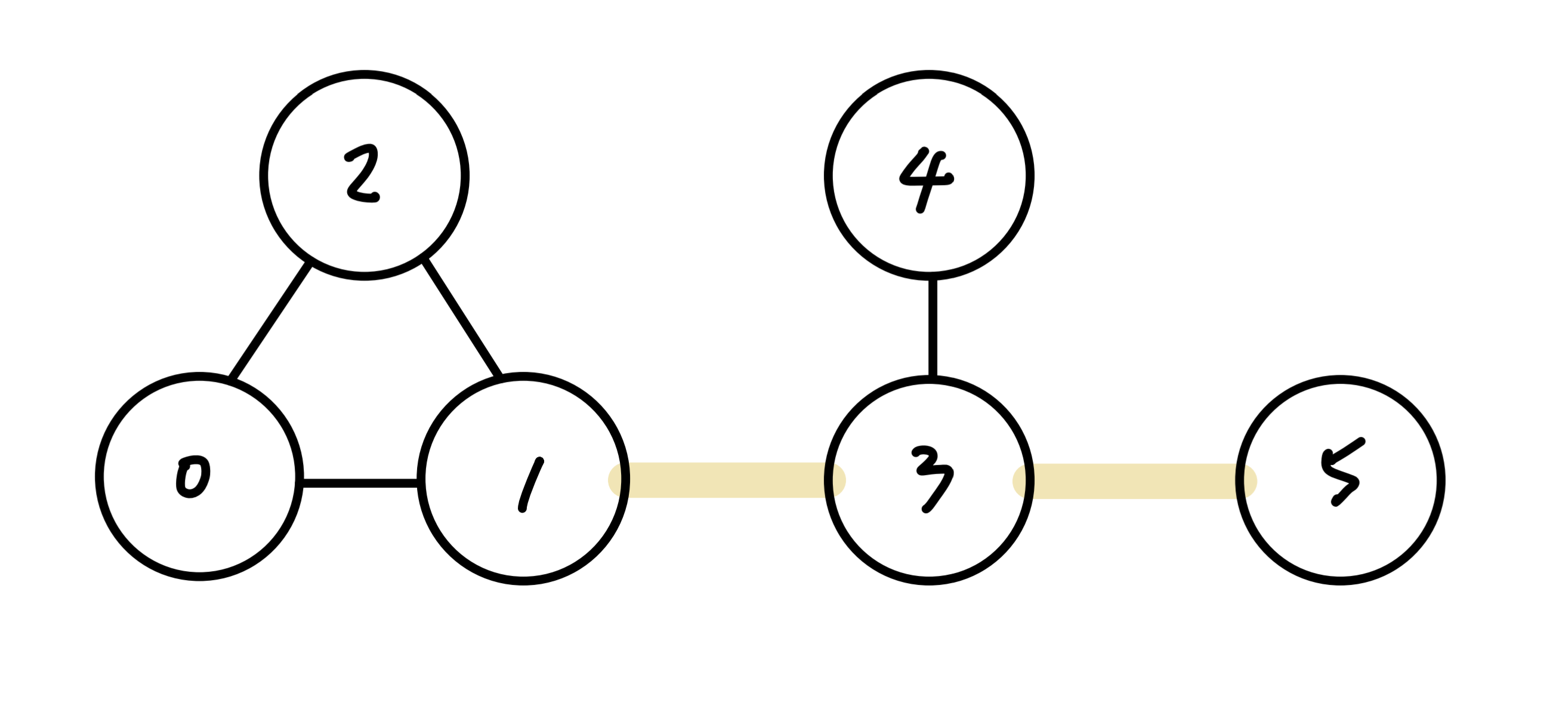
We need at least two tickets to travel to all the cities (for example, from 1 to 3 and from 3 to 5), hence the answer is 2.
There are two hints for this problem:
Hint 1: (You might get 3/6 with this hint)
If there isn't any cycle on the map, we can directly find the answer using the integer N and K.
In other words, you don't need to consider what the graph looks like, since we can list an equation for the answer with the integer N and K.
Hint 2 : (Complete solution. You may solve this problem with this hint)
visit[] // check whether every city has been visited.
count = 0;
while (!visit_all_cities) {
pick_one_unvisited_city(); // pick an unvisited city.
mark_free_cities(); // mark all the cities we can travel from this city without any ticket.
count++; // increase the group count.
}
ans = ? // find out the relation between the answer and the group count!
Input
The first line consists of two numbers N (1 ≤ N ≤ 100) and K (1 ≤ K ≤ N⋅(N-1)/2) - denoting that there are N cities in the world.
For the next K lines, each line contains two numbers A, B (0 ≤ A, B < N) - denoting that Domo can have a free flight between A and B (A ↔ B).
Output
Print the minimum number of tickets that Domo needs to buy to travel around all the cities.
Remember to print an '\n' at the end of the line.