| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13110 | Matrix 2 Not the Matrix 2 |
|
| 13111 | Alien Chickens and Alien Rabbits in a Same Cage |
|
| 13112 | Palindrome - Doubly Linked List |
|
| 13113 | Reverse-Level Traversal in BST |
|
Description
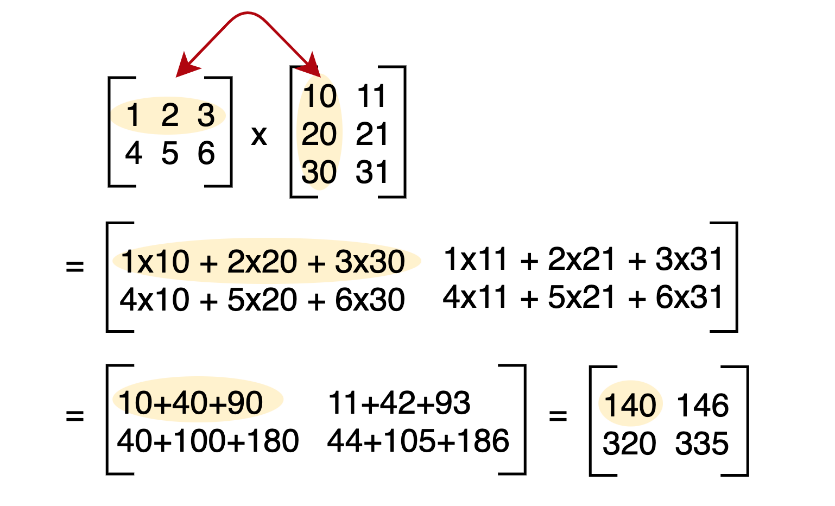
Given two matrices. Please calculate the addition, subtraction, multiplication of these two matrices.
Complete an existed class Matrix, which is used to store and calculate matrix (mathe-matics).
Matrix
Private Variables:
- row(int) represents as the size of rows in a matrix.
- col(int) represents as the size of columns in a matrix.
- val(vector<int>) use to store a mtrix’s elements.
Constructors:
- Matrix(int r, int c) – Should initalize the size of rows (row) and columns (col) to r and c.
Public Methods:
- Matrix operator+(const Matrix &other) – Should return a matrix which is the addition of the two input matrices.
- Matrix operator-(const Matrix &other) – Should return a matrix which is the subtraction of the two input matrices.
note: only when two matrices have the same size on both rows and columns can be added or subtracted.
If the conditions are not met, return a Matrix(0, 0) and print “Uncalculable”
- Matrix operator*(const Matrix &other) – Should return a matrix which is the multiplication of the two input matrices.
note: only when the size of columns in the first matrix equals to the size of rows in the second matrix can those two matrices be multiplied.
If the conditions are not met, return a Matrix(0, 0) and print “Uncalculable”
- friend ostream &operator<<(ostream &os, const Vector2 &v) – For print out a Matrix variable. (no need implement)
- void readInput() – stdin elements and put them into the val vector. (no need implement)
Input
No need to handle input. Check main.cpp for more details.
Format:
r1 c1
(r1 * c1)
r2 c2
(r2 * c2)
Output
No need to handle output. Check main.cpp for more details.
Sample Input Download
Sample Output Download
Partial Judge Code
13110.cppPartial Judge Header
13110.hTags
Discuss
Description
“Chicken-Rabbit Math Problem (雞兔同籠)” is an ancient Chinese math problem. Known the total number of heads and feet, we may tell the number of chickens and the number of rabbits respectively by solving the problem.
Let's upgrade our math problem a little bit into an alien version. Now, we have several alien chickens and alien rabbits in a same cage. Although each kind of alien chicken and alien rabbit has a different number of heads and feet, we can still get the answer by slightly changing our previos algorithm for the typical“Chicken-Rabbit Math Problem”.
To solve this alien-version problem by programming, we still can use brute-force algorithm (暴力演算法) to find out the answer directly. However, specially note, there may be serveral solutions in a same case.
Read and understand the code in main.cpp, function.h, and implment your brute-force algorithm ChickenNRabbitProblem::Solve(int chicken_h, int chicken_f, int rabbit_h, int rabbit_f) in function.cpp.
Hint:
The structure is look like the figure below.
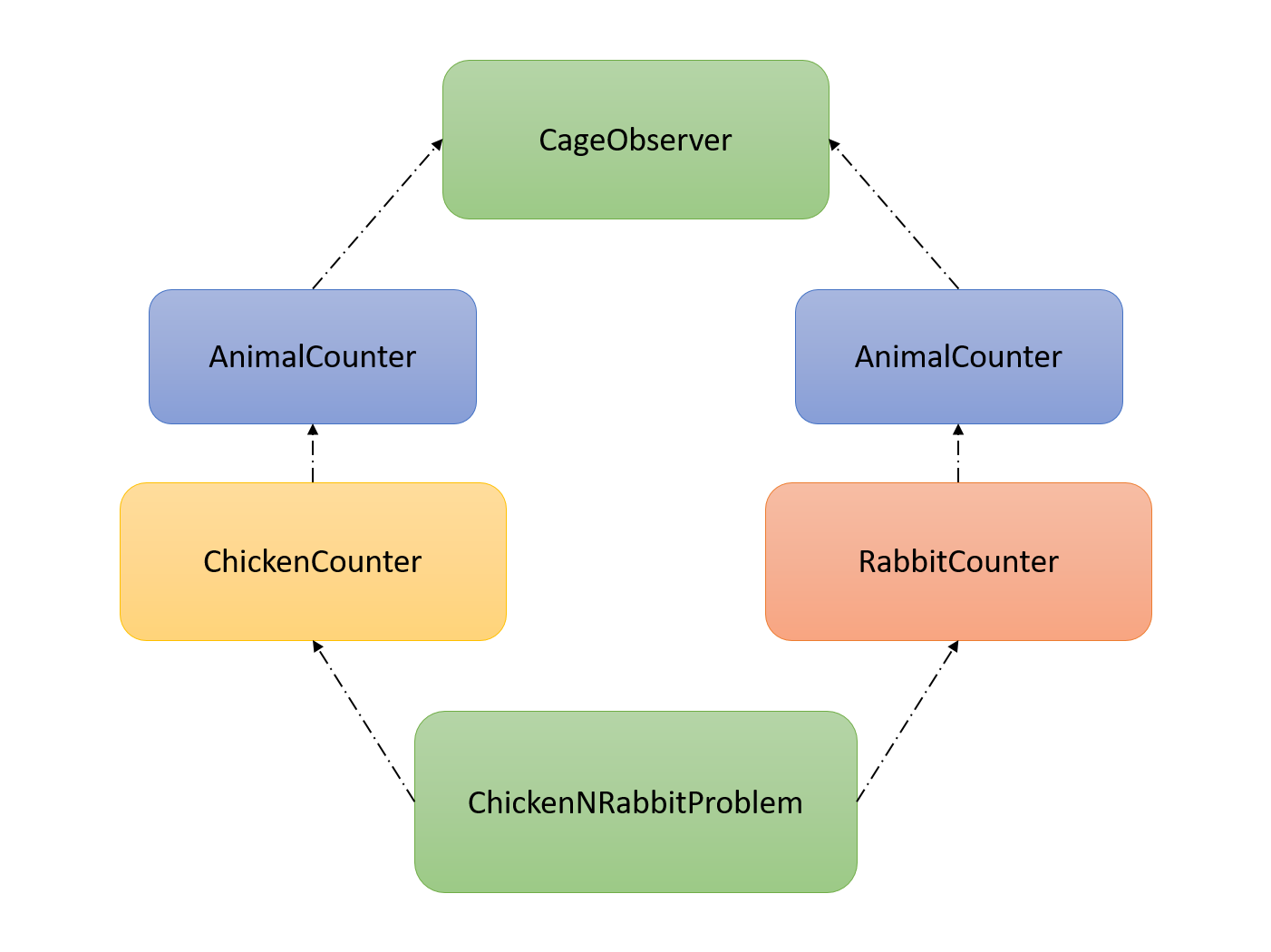
Only need to implement two methods:
- ChickenNRabbitProblem::Solve(int chicken_h, int chicken_f, int rabbit_h, int rabbit_f)
- AnimalCounter::SetHeadNFeet(int h, int f)
Use ChickenNRabbit-Problem::CheckSolution(), ChickenNRabbitProblem::PrintSolution() and functions in class ChickenCounter, RabbitCounter for help.
Input
total_head_num total_feet_num
chicken_head chicken_feet
rabbit_head rabbit_feet
note: total_head_num and total_feet_num are integers, represent as the target total number of head and feet respectively. Also, chicken_head, chicken_feet, rabbit_head, rabbit_feet are integers, represents as the number of alien chicken’s head and feet and the number of alien rabbit’s head and feet, respectively
Output
Output should follow below format:
Chicken: chicken_num_1, Rabbit: rabbit_num_1
Chicken: chicken_num_2, Rabbit: rabbit_num_2
…
Chicken: chicken_num_n, Rabbit: rabbit_num_n
note: print out all the answers of the Chicken-Rabbit Problem (sort by the number of chickens from small to large). If there are no solutions, print “no solutions” instead.
Sample Input Download
Sample Output Download
Partial Judge Code
13111.cppPartial Judge Header
13111.hTags
Discuss
Description
Doubly linked list is a more complicated singly linked list. In doubly linked list we store two addresses for our next node and previous node (shown in figure below).
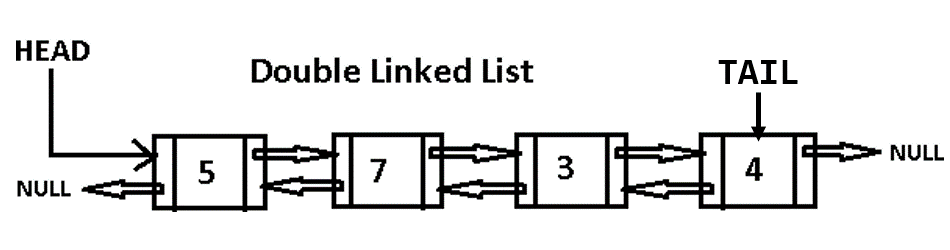
Implement the doubly linked list data structure by completing two existed classes Node and DoublyLinkedList.
Node
Public Variables:
- data(string) string data store in a node.
- next(Node*) pointer points to the next node.
- prev(Node*) pointer points to the previos node.
Constructors:
- Node(string str) – Should initalize the data (data) store in a node to str, and initialize next and prev pointer to nullptr.
DoublyLinkedList:
Public Variables:
- head(Node*) should point to the first element of the doubly linked list.
- tail(Node*) should point to the last element of the doubly linked list.
Constructors:
- The default constructor – Should initialize head and tail to nullptr.
Public Methods:
- void Insert(string str) – Should create a Node(str), and insert it into the doubly linked list, in ascending order of the string’s length.
For example:
Insert ccc // null <- ccc ->null
Insert bb // null <- bb <-> ccc -> null
Insert a // null <- a <-> bb <-> ccc -> null
Insert xx // null <- a <-> bb <-> xx <-> ccc -> null
- string StringInOrder() – Visit all the nodes in the doubly linked list from head to tail. Add up the string in every nodes’ data and return. If the doubly linked list is empty return empty string “”.
- string StringInReverse() – Visit all the nodes in the doubly linked list from tail to head. Add up the reverse string in every nodes’ data and return. If the doubly linked list is empty return empty string “”.
For example:
Insert ab // null <- ab ->null
Insert bc // null <- ab <-> bc -> null
Insert cd // null <- ab <-> bc <-> cd -> null
str // return string: abbccd
strrev // return string: dccbba
/* You Don’t Need to Implement Below Two Methods */
- bool IsPalindrome() – Return true if the doubly linked list is not empty and StringInOrder() == StringInReverse(); otherwise return false.
- bool IsEmpty() – Return true if the doubly linked list is empty (head == nullptr && tail == nullptr); otherwise, return false.
Input
There are four kinds of input command.
insert str – Call Insert(str).
ispalindrome – Call IsPalindrome().
str– Call StringInOrder().
strrev– Call StringInReverse().
Output
No need to handle output. Check main.cpp for more details.
Sample Input Download
Sample Output Download
Partial Judge Code
13112.cppPartial Judge Header
13112.hTags
Discuss
Description
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
We only implement the insertion, and reverse-level traversal methods of BST. Completing two existed classes Node and BinarySearchTree.
Node
Public Variables:
- data(int) int data stored in a node.
- left(Node*) pointer points to the left child node.
- right(Node*) pointer points to the right child node.
- parent(Node*) pointer points to the parent node.
Constructors:
- Node(int d) – Should initalize the data (data) store in a node to d, and initialize left, right and parent pointer to nullptr.
BinarySearchTree:
Public Variables:
- root(Node*) should point to the root element of the BST.
note: the root element is the first element inserted in the BST.
Constructors:
- The default constructor – Should initialize root to nullptr.
Public Methods:
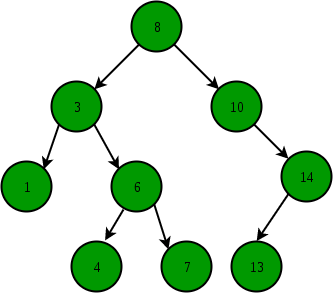
- void Insert(int i) – Should create a Node(i), and insert it into the BST. Shown as below figure.
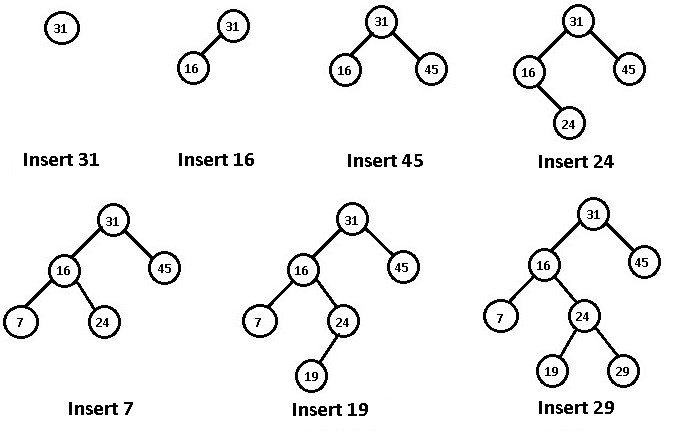
- void ReverseLevelOrderTraversal(Node* r) – Traverse each level of the tree and print all the node’s data stored in BST from left to right in reverse-level order.
note: No need to separate each of two data. Print ”/* empty */” if the BST is empty (root == nullptr).
For Example:
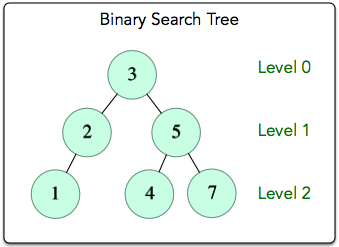
The reverse-level-order traversal is: 1->4->7->2->5->3.
hint: Queue or Vector is helpful for this implementation.
Also, to_string(int), and reverse(string.begin(), string.end()) may help.
/* You Don’t Need to Implement the Below Method */
- void InOrderTraversal() – Print all the node’s data stored in BST in order (LNR). If the list is empty print ”/* empty */”.
note: if insertion is implmented correctly, it will automatically print the data in ascending order. Also, you may use this function to check and debug.
Input
There are three kinds of input command.
insert i – Call Insert(i).
reverselevel – Call ReverseLevelOrderTraversal(root).
/* The Below Command Would Not in the Test Case Only for Debugging */
print – Call InOrderTraversal(root).
Output
No need to handle output. Check main.cpp for more details.