| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13102 | Matrix Not the Matrix |
|
| 13103 | Chickens and Rabbits in a Same Cage |
|
| 13104 | Doubly Linked List |
|
| 13105 | Give Me BTS not BST |
|
Description
Complete an existed class Matrix, which is used to store and calculate matrix (mathe-matics).
Matrix
Private Variables:
- row(int) represents as the size of rows in a matrix.
- col(int) represents as the size of columns in a matrix.
- val(vector<int>) use to store a mtrix’s elements.
Constructors:
- Matrix(int r, int c) – Should initalize the size of rows (row) and columns (col) to r and c.
Public Methods:
- Matrix operator+(const Matrix &other) – Should return a matrix which is the addition of the two input matrices.
- Matrix operator-(const Matrix &other) – Should return a matrix which is the subtraction of the two input matrices.
note: only when two matrices have the same size on both rows and columns can be added or subtracted.
If the conditions are not met, return a Matrix(0, 0) and print “Uncalculable”
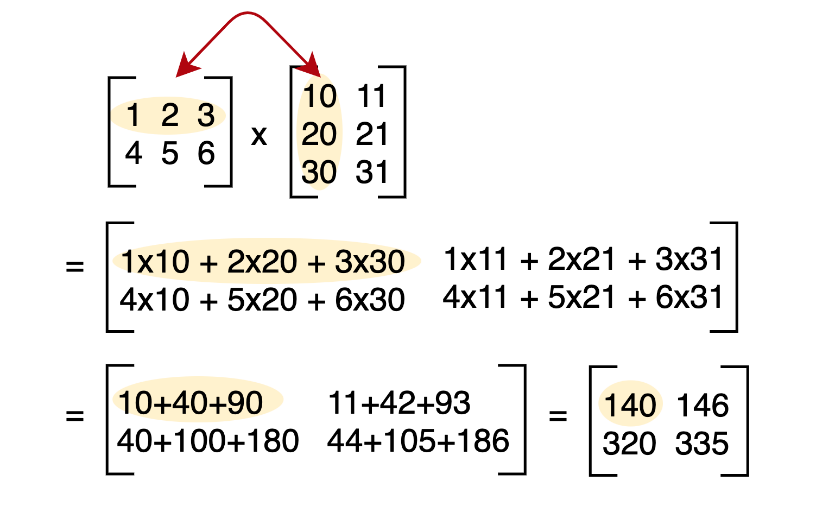
- Matrix operator*(const Matrix &other) – Should return a matrix which is the multiplication of the two input matrices.
note: only when the size of columns in the first matrix equals to the size of rows in the second matrix can those two matrices be multiplied.
If the conditions are not met, return a Matrix(0, 0) and print “Uncalculable”
- friend ostream &operator<<(ostream &os, const Vector2 &v) – For print out a Matrix variable.
Must follow below format:
[ a b c
d e f ]
note: above show a Matrix(2, 3), there is always have “[ ” in front of the first element, and “ ]” followed by the last element. Also, need two spaces “ “ in front of the first element in each row(except row[0])
- void readInput() – stdin elements and put them into the val vector. (no need implement)
Input
No need to handle input.
Four kinds of input command would be given. Check main.cpp for more details.
Output
No need to handle output. Check main.cpp for more details.
Sample Input Download
Sample Output Download
Partial Judge Code
13102.cppPartial Judge Header
13102.hTags
Discuss
Description
“Chicken-Rabbit Math Problem (雞兔同籠)” is an ancient Chinese math problem. Known the total number of heads and feet, we may tell the number of chickens and the number of rabbits respectively by solving the problem.
To solve this problem by programming, we may use brute-force algorithm (暴力演算法) to find out the answer directly. Read and understand the code in main.cpp, function.h, and implment your brute-force algorithm ChickenNRabbitProblem::Solve() in function.cpp.
Hint:
The structure is look like the figure below.
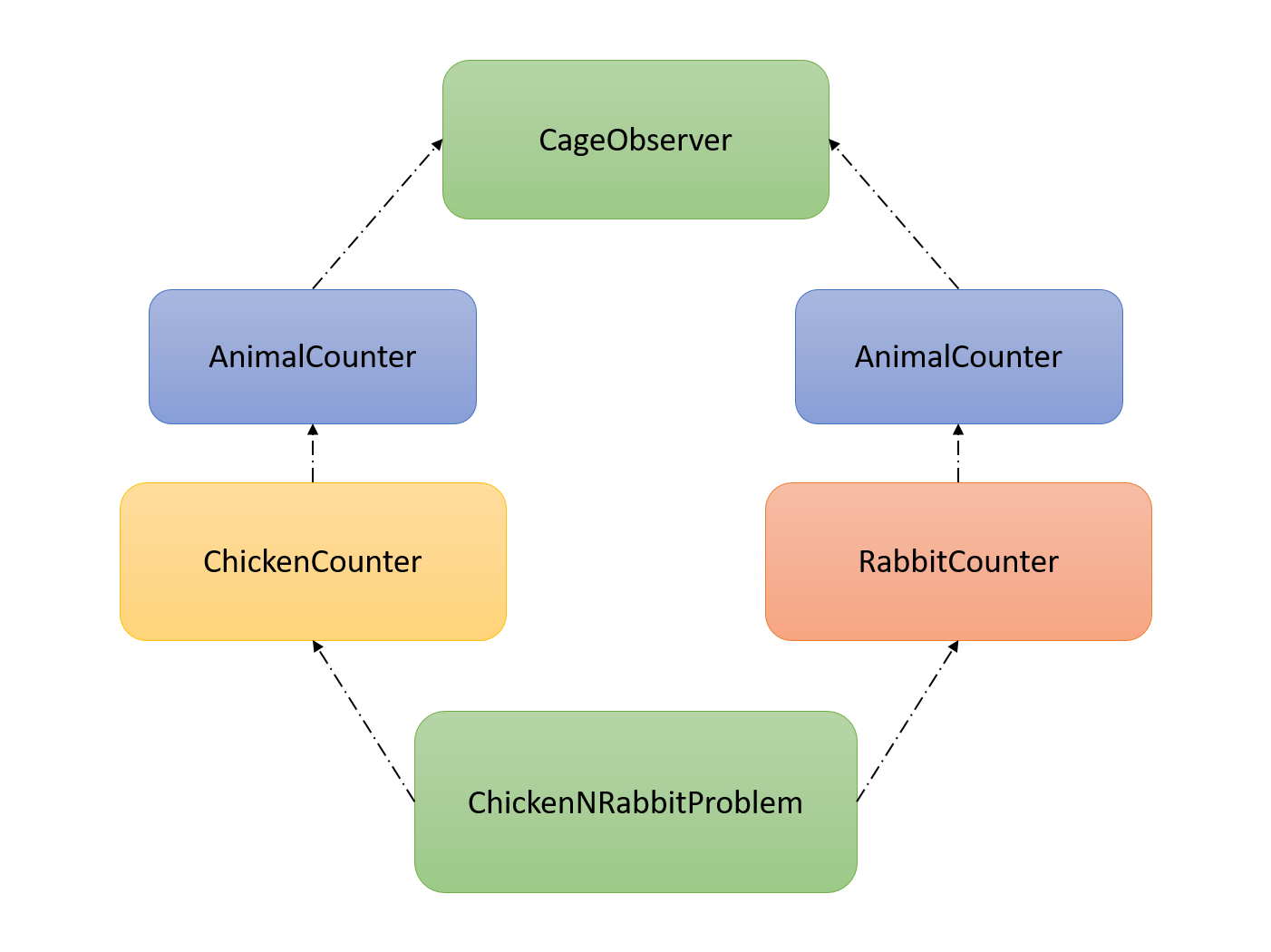
Only need to implement ChickenNRabbitProblem::Solve(). Use ChickenNRabbit-Problem:: CheckSolution (), ChickenNRabbitProblem::PrintSolution() and functions in class ChickenCounter, RabbitCounter for help.
Input
head_num feet_num
note: head_num and feet_num are integers, represent as the target total number of head and feet respectively.
Output
Output should follow below format:
Chicken: chicken_num, Rabbit: rabbit_num
note: chicken_num and rabbit_num represent as the answer of the Chicken-Rabbit Problem. If there is no solutions, print “no solutions” instead.
For example:
Input:
2 6
Output:
Chicken: 1, Rabbit: 1
Input:
2 5
Output:
no solutions
Sample Input Download
Sample Output Download
Partial Judge Code
13103.cppPartial Judge Header
13103.hTags
Discuss
Description
Doubly linked list is a more complicated singly linked list. The difference is, in singly linked list, we only store an address for our next node.
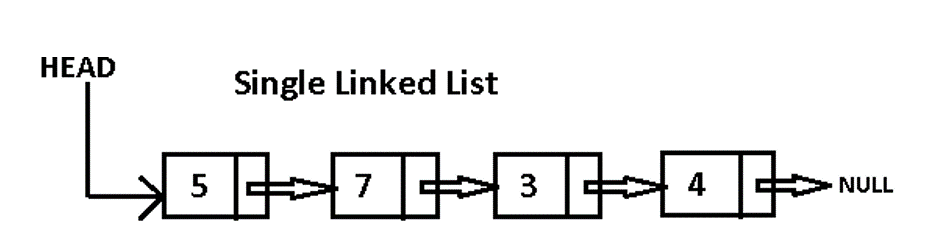
But, in doubly linked list we store two addresses for our next node and previous node (shown in figure below).
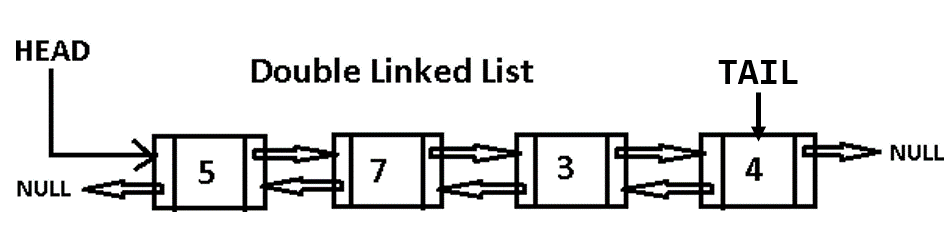
Implement the doubly linked list data structure by completing two existed classes Node and DoublyLinkedList.
Node
Public Variables:
- data(string) string data store in a node.
- next(Node*) pointer points to the next node.
- prev(Node*) pointer points to the previos node.
Constructors:
- Node(string str) – Should initalize the data (data) store in a node to str, and initialize next and prev pointer to nullptr.
DoublyLinkedList:
Public Variables:
- head(Node*) should point to the first element of the doubly linked list.
- tail(Node*) should point to the last element of the doubly linked list.
Constructors:
- The default constructor – Should initialize head and tail to nullptr.
Public Methods:
- void Insert(string str) – Should create a Node(str), and insert it into the doubly linked list, in ascending order of the string’s length.
For example:
Insert ccc // null <- ccc ->null
Insert bb // null <- bb <-> ccc -> null
Insert a // null <- a <-> bb <-> ccc -> null
Insert xx // null <- a <-> bb <-> xx <-> ccc -> null
- Node* Find(string str) – Return the address of the first node found in order which data is equal to str. If can’t find any, return nullptr.
- void Delete(string str) – Delete the first node found in order which data is equal to str. If can’t find any, do nothing.
hint: use Find().
/* You Don’t Need to Implement Below Three Methods */
- void TraversalInOrder() – Print all the node’s data stored in doubly linked list in order. If the list is empty print ”/* empty */”.
- void TraversalInReverse() – Print all the node’s data stored in doubly linked list in reverse order. If the list is empty print ”/* empty */”.
- bool IsEmpty() – Return true if the doubly linked list is empty (head == nullptr && tail == nullptr); otherwise, return false.
Input
There are five kinds of input command.
insert str – Call Insert(str).
delete str – Call Delete(str).
find str – Call Find(str).
print – Call TraversalInOrder().
reverse – Call TraversalInReverse().
Output
No need to handle output. Check main.cpp for more details.
Sample Input Download
Sample Output Download
Partial Judge Code
13104.cppPartial Judge Header
13104.hTags
Discuss
Description
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
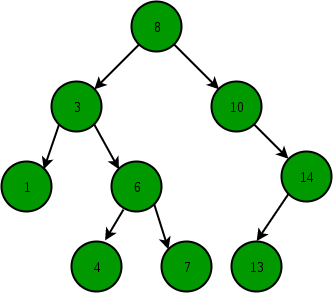
ref: https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
video: https://youtu.be/qYo8BVxtoH4
We only implement the insertion, search, and some traversal methods of BST. Completing two existed classes Node and BinarySearchTree.
Node
Public Variables:
- data(int) int data stored in a node.
- left(Node*) pointer points to the left child node.
- right(Node*) pointer points to the right child node.
- parent(Node*) pointer points to the parent node.
Constructors:
- Node(int d) – Should initalize the data (data) store in a node to d, and initialize left, right and parent pointer to nullptr.
BinarySearchTree:
Public Variables:
- root(Node*) should point to the root element of the BST.
note: the root element is the first element inserted in the BST.
Constructors:
- The default constructor – Should initialize root to nullptr.
Public Methods:
- void Insert(int i) – Should create a Node(i), and insert it into the BST. Shown as below figure.
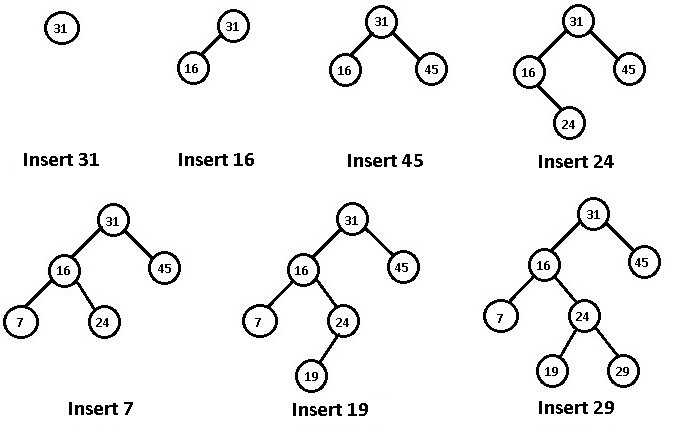
- Node* FindNode(int i) – Return the address of the node which data is equal to i. If can’t find any, return nullptr.
- Node* FindMinNode(Node *r) – Return the address of the node which data is the minimum in BST. If BST is empty, return nullptr.
- Node* FindMaxNode(Node *r) – Return the address of the node which data is the maximum in BST. If BST is empty, return nullptr.
- void LevelOrderTraversal(Node* r) – Traverse each level of the tree from the root downward, and at each level from left to right. Print all the node’s data stored in BST in order.
note: each two data is separated by a return value. Print ”/* empty */” if the BST is empty (root == nullptr).
For Example:
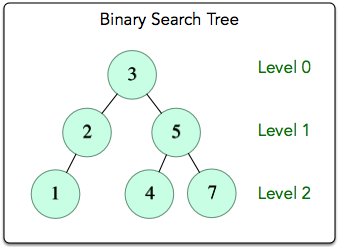
The level-order traversal is: 3->2->5->1->4->7.
hint: Queue or Vector is helpful for this implementation.
ref: https://www.hackerrank.com/challenges/30-binary-trees/problem?h_r=internal-search
/* You Don’t Need to Implement the Below Method */
- void InOrderTraversal() – Print all the node’s data stored in BST in order (LNR). If the list is empty print ”/* empty */”.
note: if insertion is implmented correctly, it will automatically print the data in ascending order. Also, you may use this function to check and debug.
Input
There are six kinds of input command.
insert i – Call Insert(i).
find i – Call FindNode(i).
min – Call FindMinNode(root).
max – Call FindMaxNode(root).
print – Call InOrderTraversal(root).
level – Call LevelOrderTraversal(root).
Output
No need to handle output. Check main.cpp for more details.